Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của hai đường chéo.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của hai đường chéo.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.

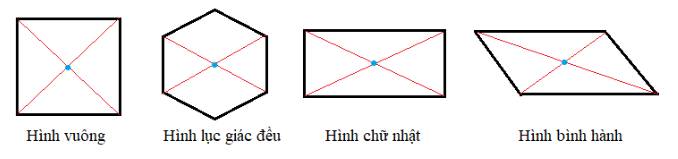
- Tâm đối xứng của hình vuông là giao điểm của hai đường chéo.
- Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.
- Tâm đối xứng của hình chữ nhật là giao điểm của hai đường chéo.
- Tâm đối xứng của hình bình hành là giao điểm của hai đường chéo.
Các hình không có tâm đối xứng: Tam giác đều, hình thang cân.

Các phát biểu về đối xứng hình học như sau:
A. Hình tròn: Hình tròn có vô số trục đối xứng và 1 tâm đối xứng. Điều này đúng.
B. Hình vuông: Hình vuông có 4 trục đối xứng, tương ứng với 4 đường đối xứng qua các đỉnh của hình vuông. Điều này cũng đúng.
C. Hình tam giác đều: Hình tam giác đều có 3 trục đối xứng và 1 tâm đối xứng. Điều này cũng đúng.
D. Hình lục giác đều: Hình lục giác đều có 1 tâm đối xứng và 6 trục đối xứng, tương ứng với 6 đường đối xứng qua các đỉnh của hình lục giác đều. Điều này cũng đúng.
Vậy tất cả các phát biểu đều đúng. 😊
hình tam giác
tick cho mik nha