

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



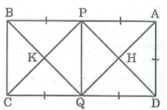
* Xét tứ giác APQD, ta có: AB // CD (gt) hay AP // QD
AP = 1/2 .AB (gt)
QD = 1/2 CD (gt)
AB= CD (vì ABCD là hình chữ nhật)
Suy ra: AP = QD
Hay tứ giác APQD là hình bình hành.
Lại có: ∠ A = 90 0 (vì tứ giác ABCD là hình chữ nhật)
Suy ra tứ giác APQD là hình chữ nhật.
Mà AD = AP = 1/2 AB
Vậy tứ giác APQD là hình vuông.
⇒ AQ ⊥ PD (t/chất hình vuông) ⇒ ∠ (PHQ) = 90 0 (1)
HP = HQ (t/chất hình vuông)
* Xét tứ giác PBCQ, ta có: AB // CD hay BP //CQ
PB = 1/2 AB (gt)
CQ = 1/2 CD (gt)
AB = CD do ABCD là hình chữ nhật
Suy ra: PB = CQ nên tứ giác PBCQ là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau)
Lại có: ∠ B = 90 0 (vì ABCD là hình chữ nhật) suy ra tứ giác PBCQ là hình chữ nhật
PB = BC ( vì cùng bằng AD = 1/2 AB)
Vậy tứ giác PBCQ là hình vuông
⇒ PC ⊥ BQ (t/chất hình vuông) ⇒ ∠ (PKQ) = 90 0 (2)
PD là tia phân giác ∠ (APQ) ( t/chất hình vuông)
PC là tia phân giác ∠ (QPB) (t/chất hình vuông)
Suy ra: PD ⊥ PC (t/chất tia phân giác của hai góc kề bù) ⇒ ∠ (HPK) = 90 0 (3)
Từ (1), (2) và (3) suy ra tứ giác PHQK là hình vuông.

Xét tứ giác APQD có
AP//QD
AP=QD
DO đó: APQD là hình bình hành
mà AP=AD
nên APQD là hình thoi
mà \(\widehat{PAD}=90^0\)
nên APQD là hình vuông
=>Hai đường chéo AQ và PD vuông góc với nhau tại trung điểm của mỗi đường và bằng nhau
=>H là trung điểm chung của AQ và PD và AQ vuông góc PD tại H
Xét tứ giác BPQC có
BP//QC
BP=QC
Do đó: BPQC là hình bình hành
mà BP=BC
nên BPQC là hình thoi
=>BQ vuông góc với CP tại trung điểm của mỗi đường
hay K là trung điểm chung của BQ và CP
Xét ΔDPC có
PQ là đường trung tuyến
PQ=CD/2
Do đó: ΔDPC vuông tại P
Xét tứ giác PHQK có
\(\widehat{PHQ}=\widehat{PKQ}=\widehat{HPK}=90^0\)
Do đó: PHQK là hình chữ nhật
mà PH=QH
nên PHQK là hình vuông

a: Xét tứ giác APQD có
AP//QD
AP=QD
Do đó: APQD là hình bình hành
mà AP=AD
nên APQD là hình thoi
mà \(\widehat{PAD}=90^0\)
nên APQD là hình vuông

a: Xét tứ giác APQD có
AP//QD
AP=QD
Do đó: APQD là hình bình hành
mà AP=AD
nên APQD là hình thoi
b: Xét tứ giác PBQD có
PB//QD
PB=QD
Do đó: PBQD là hình bình hành
Suy ra: PD//QB và PD=QB(1)
Xét tứ giác BPQC có
BP//QC
BP=QC
Do đó: BPQC là hình bình hành
mà BP=BC
nên BPQC là hình thoi
=>PC và QB cắt nhau tại trung điểm của mỗi đường
hay K là trung điểm của BQ
=>KQ=BQ/2(2)
Ta có: APQD là hình thoi
nên AQ và PD vuông góc với nhau tại trung điểm của mỗi đường
=>I là trung điểm của PD
=>IP=PD/2(3)
Từ (1), (2) và (3) suy ra IP//QK và IP=QK
hay IPKQ là hình bình hành
mà \(\widehat{PIQ}=90^0\)
nên IPKQ là hình chữ nhật