Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi I, K lần lượt là giao điểm của AC với ED và DF với AC. Gọi a,b là chiều dài, chiều rộng của hình chữ nhật. Kẻ EN, DM vuông góc với AC (N, M thuộc AC).
Ta có diện tích tam giác AED bằng ¼ ab, diện tíchtam giác FCD bằng ¼ ab, suy ra diện tích tứ giác EBFD bằng ½ ab. (*)
Ta lại có, SABC =SAEI + SEBFKI + SFKC = ½ AB (**)
Từ (*) và (**) suy ra SDIK = SAEI + SFKC
Lập luận tương tự ta suy ra SEBFKI = SAID + SCKD.
Từ đó suy ra 2(SAEI + SFKC) + 2(SAID + SCKD)= SABCD (tức là bằng a/b) (1)
DM là đường cao trong tam giác vuông ACD nên (1/DM)2=(1/a)2+(1/b)2
Tương dương DM= (ab)2/(a2+b2).
Gọi O là trung điểm của AC.
Ta có tam giác EDO đồng dạng tam giấcEO(g,g,g)
Suy ra EN/AE = EO/AO =(1/2b)/(1/2AC)=b/AC
Tương đương EN=b×AE/AC= (b×1/2a)/AC =
ab/2 a 2 + b 2
Từ đó, ta có SAID = ½ DM×AI= ½(ab)2/(a2+b2)×AI.
Suy ra SAID/SAEI= 2ab/2 a 2 + b 2
Làm tương tự để xác định tỉ số SDKC/SBKC
Sau đó rút ra gia trị của tổng diện tích các tam giác(phân gạch chéo)

Bài giải : Diện tích tam giác ABD là:
\(\frac{12x\left(12:2\right)}{2}\) = 36 (cm2)
Diện tích hình vuông ABCD là:
36 x 2 = 72 (cm2)
Diện tích hình vuông AEOK là:
72 : 4 = 18 (cm2)
Do đó : OE x OK = 18 (cm2)
r x r = 18 (cm2)
Diện tích hình tròn tâm O là:
18 x 3,14 = 56,92 (cm2)
Diện tích tam giác MON = r x r : 2 = 18 : 2 = 9 (cm2)
Diện tích hình vuông MNPQ là:
9 x 4 = 36 (cm2)
Vậy diện tích phần gạch chéo là:
56,52 - 36 = 20,52 (cm2)
Đáp số: 20,52 cm2
Chúc các bạn học tốt nhé! Kì thi cuối học kì 2 cũng đã tới, em xin chúc các anh chị Trung học, chị chúc các em Tiểu học và mình cũng chúc các bạn thi đạt điểm cao nhé!
Bài giải : Diện tích tam giác ABD là:
(12 x (12 : 2))/2 = 36 (cm2)
Diện tích hình vuông ABCD là:
36 x 2 = 72 (cm2)
Diện tích hình vuông AEOK là:
72 : 4 = 18 (cm2)
Do đó : OE x OK = 18 (cm2)
r x r = 18 (cm2)
Diện tích hình tròn tâm O là:
18 x 3,14 = 56,92 (cm2)
Diện tích tam giác MON = r x r : 2 = 18 : 2 = 9 (cm2)
Diện tích hình vuông MNPQ là:
9 x 4 = 36 (cm2)
Vậy diện tích phần gạch chéo là:
56,52 - 36 = 20,52 (cm2)
Đáp số: 20,52 cm2
Chúc các bạn học tốt nhé! Kì thi cuối học kì 2 cũng đã tới, em xin chúc các anh chị Trung học, chị chúc các em Tiểu học và mình cũng chúc các bạn thi đạt điểm cao nhé!

Cho hai hình vuông ABCD và MNPQ như trong hình vẽ. Biết BD = 12 cm. Hãy tính diện tích phần gạch chéo.
Bài giải : Diện tích tam giác ABD là: (12 x (12 : 2))/2 = 36 (cm2) Diện tích hình vuông ABCD là: 36 x 2 = 72 (cm2) Diện tích hình vuông AEOK là: 72 : 4 = 18 (cm2) Do đó : OE x OK = 18 (cm2) r x r = 18 (cm2) Diện tích hình tròn tâm O là: 18 x 3,14 = 56,92 (cm2) Diện tích tam giác MON = r x r : 2 = 18 : 2 = 9 (cm2) Diện tích hình vuông MNPQ là: 9 x 4 = 36 (cm2) Vậy diện tích phần gạch chéo là: 56,52 - 36 = 20,52 (cm2) |
Mình độ bạn này copy rồi chép vô nè chứ ko có ai có tốc độ nhanh như thế

Cạnh hình vuông là:32:4=8 (cm)
Đoạn thẳng MP là:8:2=4 (cm)
đoạn thẳng QN dài là: 4*2 =8 (cm)
Diện tích phần gạch chéo là: 8*4:2=16(cm)
Đáp số:16cm
Cạnh hình vuông là:
32:4=8(cm)
Đoạn thẳng MP là :8:2=4(cm)
Đoạn thẳng Qn dài là:4x2=8(cm)
Diện tích phần gạch chéo là:8x4:2=16(cn)
Đáp số:16cm

Vì các hình thang vuông PQMA, QMBC, QPNC, PNDA bằng nhau nên:
MQ = NP = QP = 4cm và CN = AD.
Mặt khác AD = NP + QM = 4+4 = 8 (cm)
Do đó : CN = AD = 8cm.
Diện tích hình thang vuông PQCN là : (CN + PQ) x NP : 2 = (8+4) x 4 : 2 = 24 (cm2)
Suy ra diện tích hinh chữ nhật ABCD là: 24 x 4 = 96 (cm2)

Bài giải:
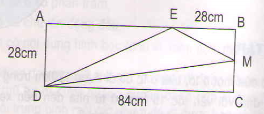
a) Chu vi hình chữ nhật ABCD là:
(84 + 28) x 2 = 224 (cm)
b) Diện tích hình thang EBCD là:
x 28 = 1568 (cm2)
c) Ta có BM = MC = 28 : 2 = 14 (cm)
Diện tích hình tam giác EBM là:
= 196 (cm2)
Diện tích tam giác DMC là:
= 588 (cm2)
Diện tích hình tam giác EDM là: 1568 - (196 + 588) = 784 (cm2)
Đáp sô: a) 224cm2 ; b) 1568cm2; c) 784cm2
Bài giải:
a) Chu vi hình chữ nhật ABCD là:
(84 + 28) x 2 = 224 (cm)
b) Diện tích hình thang EBCD là:
x 28 = 1568 (cm2)
c) Ta có BM = MC = 28 : 2 = 14 (cm)
Diện tích hình tam giác EBM là:
= 196 (cm2)
Diện tích tam giác DMC là:
= 588 (cm2)
Diện tích hình tam giác EDM là: 1568 - (196 + 588) = 784 (cm2)
Đáp sô: a) 224cm2 ; b) 1568cm2; c) 784cm2
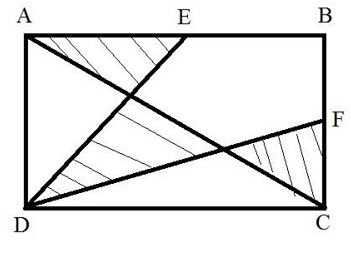
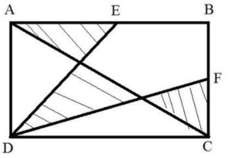





Gọi I, K lần lượt là giao điểm của AC với ED và DF với AC. Gọi a,b là chiều dài, chiều rộng của hình chữ nhật. Kẻ EN, DM vuông góc với AC (N, M thuộc AC). Ta có diện tích tam giác AED bằng 1/4 ab, diện tíchtam giác FCD bằng 1/4ab, suy ra diện tích tứ giác EBFD bằng 1/2 ab. (*)
Ta lại có, SABC =SAEI + SEBFKI + SFKC = 1/2 AB (**) Từ (*) và (**) suy ra SDIK = SAEI + SFKC Lập luận tương tự ta suy ra SEBFKI = SAID + SCKD. Từ đó suy ra 2(SAEI + SFKC) + 2(SAID + SCKD)= SABCD (tức là bằng a/b) (1) DM là đường cao trong tam giác vuông ACD nên ( 1 / D M ) 2 = ( 1 / a ) 2 + ( 1 / b ) 2 Tương dương D M = ( a b ) 2 / ( a 2 + b 2 ) . Gọi O là trung điểm của AC. Ta có tam giác EDO đồng dạng tam giấcEO(g,g,g) Suy ra EN/AE = EO/AO =(1/2b)/(1/2AC)=b/AC Tương đương EN=b×AE/AC= ( b × 1 / 2 a ) / A C = a b / 2 ( a 2 + b 2 ) Từ đó, ta có S A I D = 1 / 2 D M × A I = 1 / 2 ( a b ) 2 / ( a 2 + b 2 ) × A I . Suy ra S A I D / S A E I = 2 a b / 2 ( a 2 + b 2 ) Làm tương tự để xác định tỉ số SDKC/SBKC Sau đó rút ra gia trị của tổng diện tích các tam giác(phân gạch chéo)