Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

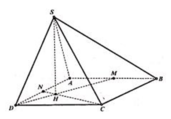
S A B C D M N H K
Thế tích của khối chóp S.CDNM :
\(S_{CDNM}=S_{ABCD}-S_{AMN}-SBC\)
\(=AB^2-\frac{1}{2}AM.AN-\frac{1}{2}BC.BM\)
\(=a^2-\frac{a^2}{8}-\frac{a^2}{4}=\frac{5a^2}{8}\)
Vậy \(V_{SCDNM}=\frac{1}{3}S_{CDNM.SH}=\frac{5\sqrt{3}a^2}{24}\)
Khoảng cách giữa 2 đường thẳng DM và SC
\(\Delta ADM=\Delta DCN\Rightarrow\widehat{ADM}=\widehat{DCN}\Rightarrow DM\perp CN\)
Kết hợp với điều kiện :
\(DM\perp SH\Rightarrow DM\perp\left(SHC\right)\)
Hạ \(HK\perp SC\left(K\in SC\right)\Rightarrow HK\)là đoạn vuông góc chung của DM và SC
Do đó :
\(d\left(DM,SC\right)=HK\)
Ta có :
\(\begin{cases}HC=\frac{CD^2}{CN}=\frac{2a}{\sqrt{5}}\\HK=\frac{SH.HC}{\sqrt{SH^2+HC^2}}=\frac{2\sqrt{3}a}{\sqrt{19}}\end{cases}\)
\(\Rightarrow d\left(DM,SC\right)=\frac{2\sqrt{3}a}{\sqrt{19}}\)
cậu ơi, hướng dẫn giúp tớ bài tương tự này với: cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, góc giữa SD và mặt phẳng ABCD là 45 độ, SA vuông góc (ABCD). M là trung điểm BC. Tính khoảng cách DM và SC
cảm ơn c nhiều nhiều.

A N B C H K S
Theo giả thiết, \(HA=HC=\frac{1}{2}AC=a\) và \(SH\perp\left(ABC\right)\)
Xét \(\Delta v.ABC\) ta có : \(BC=AC.\cos\widehat{ACB}=2a\cos30^0=\sqrt{3}a\)
Do đó : \(S_{\Delta.ABC}=\frac{1}{2}AC.BC.\sin\widehat{ACB}=\frac{1}{2}.2a.\sqrt{3}a.\sin30^0=\frac{\sqrt{3}a^2}{2}\)
Vậy \(V_{S.ABC}=\frac{1}{3}SH.S_{ABC}=\frac{1}{3}.\sqrt{2}a.\frac{\sqrt{3}}{2}a^2=\frac{\sqrt{6}a^3}{6}\)
Vì CA=2HA nên d(C,(SAB))=2d(H, (SAB)) (1)
Gọi N là trung điểm của Ab, ta có HN là đường trung bình của tam giác ABC
Do đó HN//BC suy ra AB vuông góc với HN.
Lại có AB vuông góc với Sh nên AB vuông góc với mặt phẳng (SHN).
Do đó mặt phẳng (SAB) vuông góc với mặt phẳng (SHN).
Mà Sn là giao tuyến của 2 mặt phẳng vừa nêu, nên trong mặt phẳng (SHN), hạ HK vuông góc với SN, ta có HK vuông góc với mặt phẳng (SAB)
Vì vậy d(J, (SAB)) = HK. Kết hợp với (1), suy ra d(C. (SAB))=2HK (2)
Vì \(SH\perp\left(ABC\right)\) nên \(SH\perp HN\), xét tam giác v.SHN, ta có :
\(\frac{1}{HK^2}=\frac{1}{SH^2}+\frac{1}{HN^2}=\frac{1}{2a^2}+\frac{1}{HN^2}\)
Vì HN là đường trung bình của tam giác ABC nên \(HN=\frac{1}{2}BC=\frac{\sqrt{3}a}{2}\)
Do \(\frac{1}{HK^2}=\frac{1}{2a^2}+\frac{4}{3a^2}=\frac{11}{6a^2}\) suy ra \(HK=\frac{\sqrt{66}a}{11}\) (3)
Thế (3) vào (2) ta được \(d\left(C,\left(SAB\right)\right)=\frac{\sqrt{66}a}{11}\)


\(V_{ABSI}=V_{S.ABI}=\dfrac{1}{2}V_{S.ABCD}=\dfrac{a^3}{9}\)

S D A H B M C I N
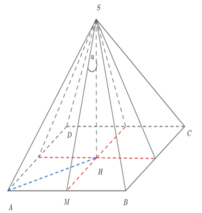
Gọi H là tâm của ABCD\(\Rightarrow SH\perp\left(ABCD\right)\)
M là trung điểm của BC \(\Rightarrow BC\perp\left(SHM\right)\)
Do các mặt bên tạo với đáy cùng 1 góc => \(\widehat{SHM}\) bằng góc tạo bởi 2 mặt bên với đáy
Tính được \(SH=\frac{a\sqrt{3}}{2}'HM=\frac{a}{2}\)
\(\tan\widehat{SMH}=\frac{SH}{MH}=\sqrt{3}\Rightarrow\widehat{SMN}=60^0\)
Lập luận được tâm khối cầu là điểm I của SH với trung trực SC trong (SHC)
Tính được bán kính khối cầu do tam giác SNI đồng dạng với tam giác SHC
\(\Rightarrow SI=\frac{SN.SC}{SH}=\frac{5a}{4\sqrt{3}}\)
Vậy \(V=\frac{4}{3}\pi R^2=\frac{125a^3\sqrt{3}\pi}{432}\)



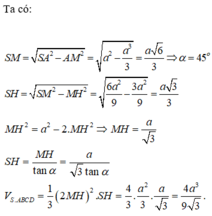

Đáp án C