Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

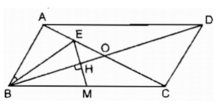
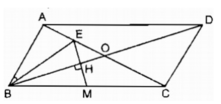
Theo chứng minh ở câu a. △ AEB đồng dạng △ ABC theo tỉ số k = 1/2 nên dễ thấy BE = 1/2 BC hay BE = BM
Suy ra: ΔBEM cân tại B.
Xét tam giác EBC có: 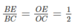
Suy ra: OB là đường phân giác góc EBC
BO là đường phân giác góc ở đỉnh của tam giác cân BEM nên BO vuông góc với cạnh đáy EM (đpcm).

Vì ABCD là hình bình hành và E là trung điểm của AO (vì BE là trung tuyến của tam giác ABO) nên ta có: AO = CO = 1/2 AC; AE = 1/2 AO.
Mặt khác, theo giả thiết AC = 2AB nên dễ thấy AB = AO và do đó AE = 1/2AB
Xét hai tam giác AEB và ABC, ta có:
Góc A chung
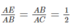
Vậy △ AEB đồng dạng △ ABC (c.g.c)
Suy ra: hai góc tương ứng bằng nhau ∠ ABE = ∠ ACB (đpcm)

a) Xét ΔANI và ΔCND có
\(\widehat{ANI}=\widehat{CND}\)(hai góc đối đỉnh)
\(\widehat{IAN}=\widehat{DCN}\left(=45^0\right)\)
Do đó: ΔANI\(\sim\)ΔCND(g-g)

a: Xét ΔAED vuông tại E và ΔCFB vuông tại F có
AD=CB
\(\widehat{ADE}=\widehat{CBF}\)
Do đó: ΔAED=ΔCFB
Suy ra AE=CF: ED=FB
Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: Xét ΔKBF vuông tại F và ΔIDE vuông tại E có
FB=ED
\(\widehat{KBF}=\widehat{IDE}\)
Do đó: ΔKBF=ΔIDE
Suy ra: KB=ID
Xét tứ giác KBID có
KB//ID
KB=ID
Do đó: KBID là hình bình hành
Suy ra: Hai đường chéo KI và BD cắt nhau tại trung điểm của mỗi đường