Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

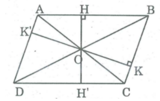
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm
* Kéo dài OH cắt cạnh CD tại H'.
Ta có OH ⊥ BC
⇒ OH' ⊥ CD và OH' = 2cm
Suy ra HH' bằng đường cao của hình bình hành.
S
A
B
C
D
= HH'.AB ⇒ ![]()
* Kéo dài OK cắt AD tại K'.
Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)
Suy ra KK' là đường cao của hình bình hành.
S
A
B
C
D
= KK'.AB ⇒ ![]()
Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).

tk hen:
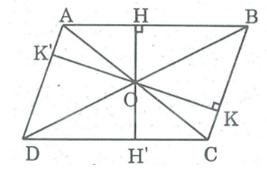
Gọi O là giao điểm hai đường chéo của hình bình hành ABCD, khoảng cách từ O đến cạnh AB là OH = 2cm , đến cạnh BC là OK = 3cm
* Kéo dài OH cắt cạnh CD tại H'.
Ta có OH ⊥ BC
⇒ OH' ⊥ CD và OH' = 2cm
Suy ra HH' bằng đường cao của hình bình hành.

![]()
* Kéo dài OK cắt AD tại K'.
Ta có: OK ⊥ BC ⇒ OK' ⊥ CD và OK' = 3 (cm)
Suy ra KK' là đường cao của hình bình hành.

![]()
Chu vi của hình bình hành ABCD là (6 + 4).2 = 20 (cm).


A B C D O 3 4 8
a) \(S_{ABCD}=8\cdot3\cdot2=72\left(cm^2\right)\)
b) Ta có: \(S_{AOB}=S_{COD}=\frac{3\cdot8}{2}=12\left(cm^2\right)\)và \(S_{AOD}=S_{COB}\)
Mà \(S_{ABCD}=S_{AOB}+S_{COD}+S_{AOD}+S_{BOC}\)
\(\Leftrightarrow2\cdot12+2\cdot2BC=72\Leftrightarrow4BC=48\Leftrightarrow BC=12\left(cm\right)\)