Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

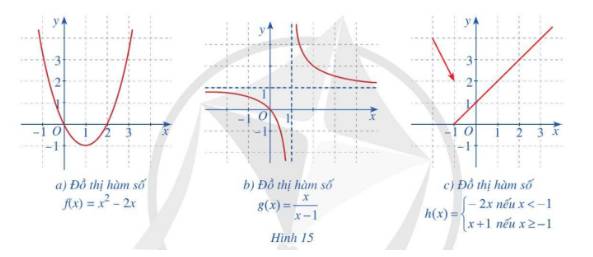
+) Hình 15a: Hàm số \(f\left( x \right) = {x^2}\;-2x\) có tập xác định \(D = \mathbb{R}.\)
Hàm số liên tục trên \(\mathbb{R}.\)
+) Hình 15b: Hàm số \(g\left( x \right) = \frac{x}{{x - 1}}\) có tập xác định \(D = \mathbb{R}\backslash \left\{ 1 \right\}.\)
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;1} \right)\)và \(\left( {1; + \infty } \right).\)
+) Hình 15c:
Với \(x\; \in \;\left( {-\infty ;-1} \right)\) có \(f\left( x \right) = -2x\) liên tục với mọi \(x\; \in \;\left( {-\infty ;-1} \right)\)
Với \(x\; \in \;\left( {-1; + \infty } \right)\) có \(f\left( x \right) = x + 1\) liên tục với mọi \(x\; \in \;\left( {-1; + \infty } \right)\)
Tại x = – 1 có
\(\begin{array}{l}\mathop {\lim }\limits_{x \to - 1} f\left( x \right) = \mathop {\lim }\limits_{x \to - 1} \left( {2x} \right) = 2.\left( { - 1} \right) = - 2\\f\left( { - 1} \right) = - 1 + 1 = 0\\ \Rightarrow \mathop {\lim }\limits_{x \to - 1} f\left( x \right) \ne f\left( { - 1} \right)\end{array}\)
Do đó hàm số không liên tục tại x = – 1.
Vậy hàm số liên tục trên các khoảng \(\left( {-\infty ;-1} \right)\)và \(\left( {-1; + \infty } \right).\)

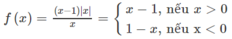
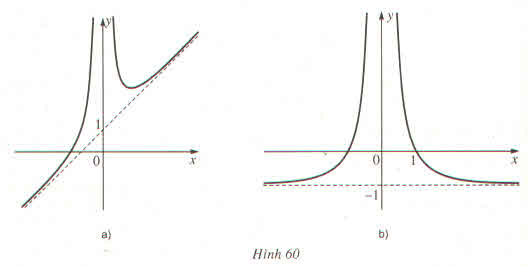
Hàm số này có tập xác định là R \ {0}
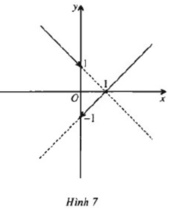
Từ đồ thị (H.7) dự đoán f(x) liên tục trên các khoảng (−∞;0), (0; +∞) nhưng không liên tục trên R. Thật vậy,
- Với x > 0, f(x) = x − 1 là hàm đa thức nên liên tục trên R do đó liên tục trên (0; +∞)
- Với x < 0, f(x) = 1 – x cũng là hàm đa thức nên liên tục trên R do đó liên tục trên (−∞; 0)
Dễ thấy hàm số gián đoạn tại x = 0 vì

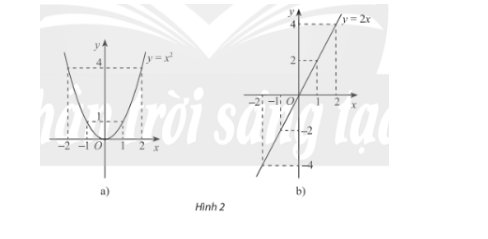
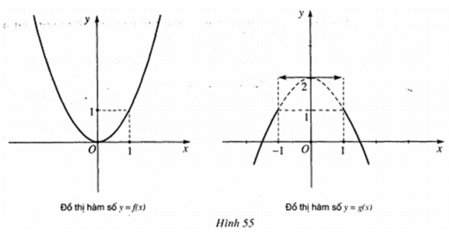
* Hàm số \(y = {x^2}\)
Nhìn đồ thị ta thấy:
+ \(y(1) = y( - 1) = 1,y(2) = y( - 2) = 4\)
+ Đồ thị hàm số đối xứng qua trục Oy.
* Hàm số \(y = 2x\)
Nhìn đồ thị ta thấy:
+ \(y(1) = - y( - 1),y(2) = - y( - 2)\)
+ Đồ thị hàm số đối xứng qua điểm O.

a) Do hoành độ giao điểm nằm trên khoảng \(\left( {0;\pi } \right)\) nên: \(\cot x = m \Leftrightarrow \cot x = \cot \alpha \Leftrightarrow x = \alpha + k\pi \)
b) Nhận xét: trên khoảng\(\left( {0;\pi } \right)\), với mọi \(m \in \mathbb{R}\) ta luôn có \(x = \alpha + k\pi \)

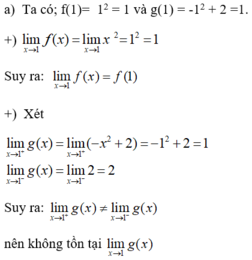
b)
+ Đồ thị của hàm số y = f(x) là đường liền nét tại điểm có hoành độ x= 1.
+ Đồ thị hàm số y = g(x) là đường không liền nét tại điểm có hoành độ x= 1.

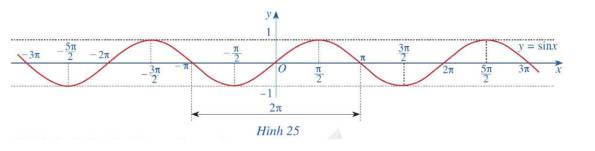
a) Tập giá trị của hàm số\(y = \sin x\) là \(\left[ { - 1;1} \right]\)
b) Đồ thị hàm số \(y = \sin x\) nhận O là tâm đối xứng.
Như vậy hàm số \(y = \sin x\) là hàm số lẻ.
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị hàm số \(y = \sin x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy, hàm số \(y = \sin x\) có tuần hoàn .
d) Hàm số \(y = \sin x\) đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k2\pi ;\frac{\pi }{2} + k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {\frac{\pi }{2} + k2\pi ;\frac{{3\pi }}{2} + k2\pi } \right)\) với \(k \in Z\)

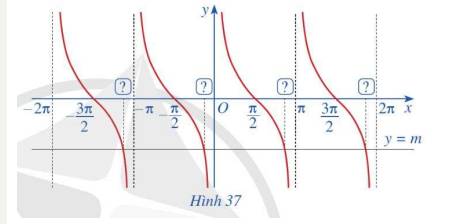
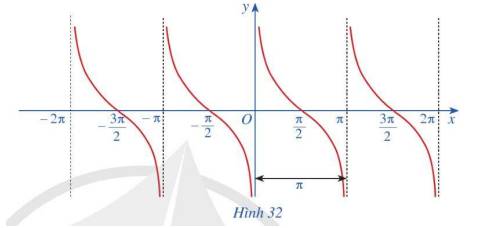
a) Tập giá trị của hàm số \(y = \cot x\)là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Hàm số \(y = \cot x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \cot x\) trên khoảng \(\left( {0;\pi } \right)\) song song với trục hoành sang phải theo đoạn có độ dài \(\pi \), ta nhận được \(y = \cot x\) trên khoảng \(\left( {\pi ;2\pi } \right)\)
Hàm số \(y = \cot x\) có tuần hoàn
d) Hàm số \(y = \cot x\)nghịch biến trên mỗi khoảng \(\left( {k\pi ;\pi + k\pi } \right),k \in Z\)

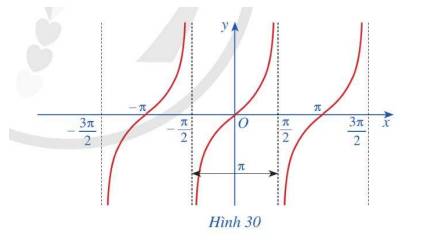
a) Tập giá trị của hàm số \(y = \tan x\) là R
b) Gốc tọa độ là tâm đối xứng của đồ thị hàm số
Như vậy, hàm số \(y = \tan x\)là hàm số lẻ
c) Bằng cách dịch chuyển đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( { - \frac{\pi }{2};\frac{\pi }{2}} \right)\) song song với trục hoành sang phải theo đoạn có độ dài π, ta nhận được đồ thị hàm số \(y = \tan x\) trên khoảng \(\left( {\frac{\pi }{2};\frac{{3\pi }}{2}} \right)\)
Như vậy, hàm số \(y = \tan x\) có tuần hoàn
d) Hàm số \(y = \tan x\)đồng biến trên mỗi khoảng \(\left( { - \frac{\pi }{2} + k\pi ;\frac{\pi }{2} + k\pi } \right)\) với \(k \in Z\)
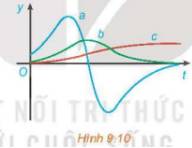

Hàm số c luôn đồng biến, tức là đạo hàm của nó phải luôn không âm, do đó hàm số b là đạo hàm của hàm số c; hàm số b đồng biến trên khoảng mà hàm số a dương và nghịch biến trên khoảng mà hàm số a âm, do đó hàm số a là đạo hàm của hàm số b.
Vậy hàm số a là hàm gia tốc, hàm số b là hàm vận tốc và hàm số c là hàm vị trí của ô tô.