Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

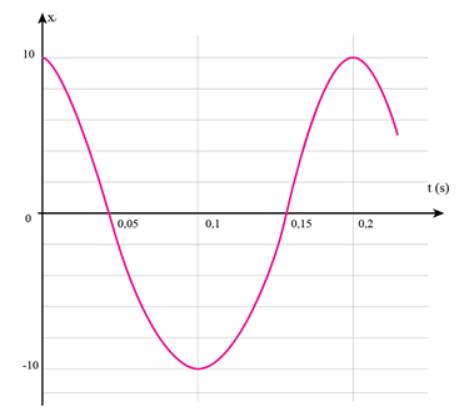
Chu kì dao động là: \(T=\dfrac{1}{f}=\dfrac{1}{5}=0,2\left(s\right)\)
Tần số góc của dao động là: \(\omega=2\pi f=10\pi\left(rad/s\right)\)
Lúc t = 0, ta có: \(\left\{{}\begin{matrix}x=A\\v=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}cos\varphi=1\\sin\varphi=0\end{matrix}\right.\Rightarrow\varphi=0\)
Phương trình dao động là: \(x=10cos\left(10\pi t\right)cm\)
Vẽ đồ thị:

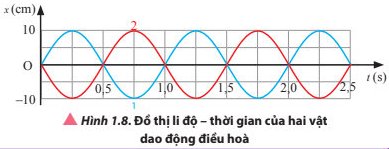
Hai dao động có cùng biên độ.
Ở cùng một thời điểm khi dao động 1 ở vị trí cân bằng thì dao động 2 ở vị trí bên và ngược lại.

a) Dao động 1 (đường màu xanh) có:
- Biên độ: A1 = 3 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
Dao động 2 (đường màu đỏ) có:
- Biên độ: A2 = 4 cm
- Chu kì: T = 6 s
- Tần số: \(f=\dfrac{1}{T}=\dfrac{1}{6}\left(Hz\right)\)
b) Hai dao động có cùng chu kì nên \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{6}=\dfrac{\pi}{3}\left(rad/s\right)\)
Độ lệch thời gian của hai dao động khi cùng trạng thái: \(\Delta t=2,5s\)
Độ lệch pha: \(\Delta\varphi=\omega.\Delta t=\dfrac{\pi}{3}\cdot2,5=150^o\)
c) Tại thời điểm 3,5 s vật 2 đang ở VTCB nên vận tốc cực đại:
\(v=\omega A_2=\text{ }\dfrac{\pi}{3}\cdot4=\dfrac{4\pi}{3}\left(cm/s\right)\)
d) Tại thời điểm 1,5 s vật 1 đang ở biên dương nên gia tốc có giá trị:
\(a=-\omega^2A_1=-\dfrac{\pi^2}{9}\cdot3=-\dfrac{\pi^2}{3}\left(cm/s^2\right)\)
Độ lớn gia tốc khi đó là \(\dfrac{\pi^2}{3}cm/s^2\)

- Từ đồ thị ta thấy:
Biên độ: \(A = 0,2\left( m \right) = 20\left( {cm} \right)\)
Chu kì: \(T = 0,4\left( s \right)\)
Tần số: \(f = \frac{1}{T} = \frac{1}{{0,4}} = 2,5\left( {Hz} \right)\)
- Tần số góc của dao động điều hoà: \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi \) (rad/s)
Từ đồ thị ta thấy lúc \(t = 0\) thì \(x = 0\) và đang đi về biên dương
\( \Rightarrow \left\{ \begin{array}{l}0 = A.\cos \varphi \\ - \omega A\sin \varphi > 0\end{array} \right. \Rightarrow \left\{ \begin{array}{l}\cos \varphi = 0\\\sin \varphi < 0\end{array} \right. \Rightarrow \varphi = - \frac{\pi }{2}\)
Phương trình dao động điều hoà: \(x = 20\cos \left( {5\pi t - \frac{\pi }{2}} \right)\) cm.
+ Thời điểm vật có li độ \(x = 0\) là:
\(\begin{array}{l}20\cos \left( {5\pi t - \frac{\pi }{2}} \right) = 0 \Leftrightarrow \cos \left( {5\pi t - \frac{\pi }{2}} \right) = 0\\ \Rightarrow 5\pi t - \frac{\pi }{2} = \frac{\pi }{2} + k\pi \Rightarrow t = \frac{1}{5} + \frac{k}{5}\,\end{array}\)
với \(k = - 1,0,1,2....\)
+ Thời điểm vật có li độ \(x = 0,1m = 10cm\) là:
\(\begin{array}{l}20\cos \left( {5\pi t - \frac{\pi }{2}} \right) = 10 \Leftrightarrow \cos \left( {5\pi t - \frac{\pi }{2}} \right) = \frac{1}{2}\\ \Rightarrow \left\{ \begin{array}{l}5\pi t - \frac{\pi }{2} = \frac{\pi }{3} + k2\pi \\5\pi t - \frac{\pi }{2} = \frac{\pi }{3} + k2\pi \end{array} \right. \Rightarrow \left\{ \begin{array}{l}t = \frac{1}{6} + \frac{{2k}}{5}\,\left( {k = 0,1,2...} \right)\\t = \frac{{ - 1}}{{30}} + \frac{{2k}}{5}\left( {k = 0,1,2...} \right)\end{array} \right.\end{array}\)

a) Biên độ dao động A=0,2 cm
Chu kì T=0,4 s
Tần số \(f = \frac{1}{T} = \frac{1}{{0,4}} = 2,5Hz\)
Tần số góc của dao động \(\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{0,4}} = 5\pi rad/s\)
b) Li độ của vật dao động tại các thời điểm t1, t2, t3 ứng với các điểm A, B, C trên đường đồ thị li độ – thời gian lần lượt là x1=-0,1 cm, x2= -0,2 cm, x3= 0 cm.
c) Vì gốc thời gian trùng với vị trí cân bằng nên li độ cũng chính là độ dịch chuyển từ vị trí cân bằng đến vị trí của vật tại các điểm A, B, C.

Biên độ: A=3
Tần số góc: pi
Chu kì: T=2pi/pi=2
Pha dao động: pi*t
Pha ban đầu: 2pi

Để xác định biên độ, tần số góc, chu kì và pha ban đầu của động, ta cần phân tích công thức của dao động và so sánh với công thức tổng quát.Công thức tổng quát của một dao động harmonic là:x = A * cos(ωt + φ)Trong đó:- x là vị trí của đối tượng tại thời điểm t.- A là biên độ của dao động.- ω là tần số góc của dao động.- t là thời gian.- φ là pha ban đầu của dao động.Trong công thức đã cho:x = -5cos(10πt + π/2)cmSo sánh với công thức tổng quát, ta có:A = -5 cm (biên độ)ω = 10π rad/s (tần số góc)φ = π/2 rad (pha ban đầu)Như vậy, biên độ của dao động là -5 cm, tần số góc là 10π rad/s, chu kì của dao động là T = 2π
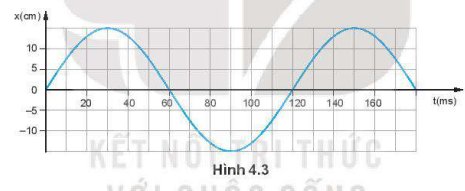
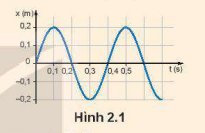


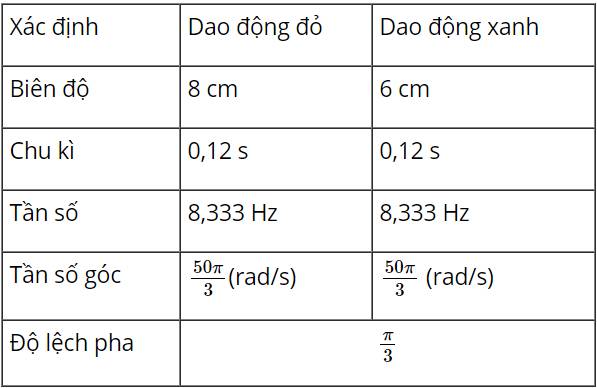
a) Biên độ A = 15 (cm)
Chu kì T = 120 (ms) = 0,12 (s)
Tần số f = \(\frac{{25}}{3}\) (Hz)
Tần số góc ω = \(\frac{{2\pi }}{T}\) = \(\frac{{2\pi }}{{0,12}}\)= \(\frac{{50\pi }}{3}\) (rad/s)
Pha ban đầu φ = \( - \frac{\pi }{2}\)
b) Phương trình dao động của vật là: x = 15cos(\(\frac{{50\pi }}{3}\)t −\(\frac{\pi }{2}\)) (cm)