Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Để tạo một biển số xe ta thực hiện các bước sau:
+ Chọn hai chữ cái cho phần đầu có 
(mỗi chữ có 26 cách chọn)
+ Chọn 5 chữ số cho phần đuôi có 
(mỗi chữ số có 10 cách chọn)
Vậy có thể tạo ra được 
biển số xe
Đáp án A
Tổng số phiếu trong hộp là 24. Gọi Ω là không gian mẫu.
* Lấy ngẫu nhiên 4 phiếu trong hộp ta có 
cách lấy hay 
Gọi A là biến cố lấy được các phiếu có đủ cả 3 loại.
Ta có các trường hợp sau:
+) 2 đỏ, 1 vàng và 1 xanh: có
cách
+) 1 đỏ, 2 vàng và 1 xanh: có 
cách
+) 1 đỏ, 1 vàng và 2 xanh: có 
cách
Do đó, 
Vậy, xác suất biến cố A là
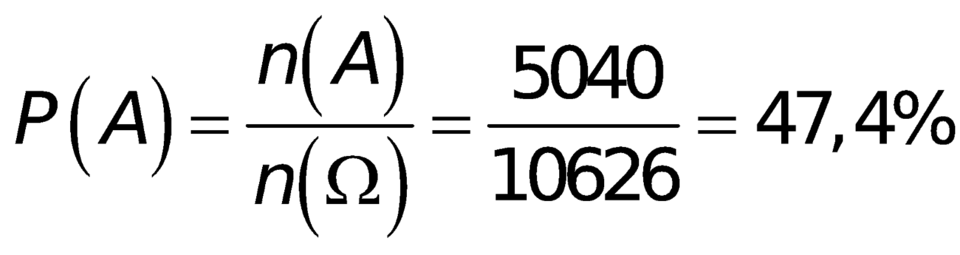
a) Do số bệnh nhân là số nguyên nên ta hiệu chỉnh như sau:
Số bệnh nhân đến khám bệnh mỗi ngày trong tháng 4 năm 2022 là:
\(n = 7 + 8 + 7 + 6 + 2 = 30\).
Gọi \({x_1};{x_2};...;{x_{30}}\) là số bệnh nhân đến khám bệnh mỗi ngày được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_7} \in \begin{array}{*{20}{l}}{\left[ {0,5;10,5} \right)}\end{array};{x_8},...,{x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array};{x_{16}},...,{x_{22}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array};\\{x_{23}},...,{x_{28}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array};{x_{29}},{x_{30}} \in \begin{array}{*{20}{l}}{\left[ {40,5;50,5} \right)}\end{array}\end{array}\)
• Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{15}} + {x_{16}}} \right)\)
Do \({x_{15}} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array},{x_{16}} \in \begin{array}{*{20}{l}}{\left[ {20,5;30,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là: \({Q_2} = 20,5\).
• Tứ phân vị thứ nhất của dãy số liệu là: \({x_8}\).
Ta có: \(n = 30;{n_m} = 8;C = 7;{u_m} = 10,5;{u_{m + 1}} = 20,5\)
Do \({x_8} \in \begin{array}{*{20}{l}}{\left[ {10,5;20,5} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 10,5 + \frac{{\frac{{30}}{4} - 7}}{8}.\left( {20,5 - 10,5} \right) = 11,125\)
• Tứ phân vị thứ ba của dãy số liệu là: \({x_{23}}\).
Ta có: \(n = 30;{n_j} = 6;C = 7 + 8 + 7 = 22;{u_j} = 30,5;{u_{j + 1}} = 40,5\)
Do \({x_{23}} \in \begin{array}{*{20}{l}}{\left[ {30,5;40,5} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 30,5 + \frac{{\frac{{3.30}}{4} - 22}}{6}.\left( {40,5 - 30,5} \right) \approx 31,3\)
b) Do \({Q_3} \approx 31,3\) nên nhận định trên hợp lí.
Đáp án D
Đặt x, y, h lần lượt là chiều dài, chiều rộng và chiều cao mỗi phòng.
Theo giả thiết, ta có x.3y = 1152 → y = 384 x
Để tiết kiệm chi phí nhất khi diện tích toàn phần nhỏ nhất.
Ta có 
Vì h không đổi nên
S
t
p
nhỏ nhất khi 
(với x > 0) nhỏ nhất.
Khảo sát 
với x > 0 ta được f(x) nhỏ nhất khi x = 24 => y = 16