Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Công của lực điện di chuyển proton: A C D = q U C D = 3 , 2 . 10 - 17 J
b. Công của lực điện trường di chuyển electron: A C D = q U C D = - 3 , 2 . 10 - 17 J

a/ Theo công thức liên hệ giữa cường độ điện trường và hiệu điện thế :
\(E=\frac{U}{d}\) ta có d = CƯỜNG ĐỘ
Suy ra \(E=\frac{U_{CD}}{CD}=\frac{100}{0,02}=\frac{5000V}{m}\)
Để tìm \(U_{AB}\), ta giả sử có một điện tích q dịch chuyển từ A đến B. Theo định nghĩa của hiệu điện thế ta có: \(U_{AB}=\frac{A_{AB}}{q}\)
Trên đoạn đường AB, lực điện trường F = qE luôn luôn vuông góc với AB nên công của lực điện trường
\(A_{AB}=0\). Ta suy ra \(U_{AB}=0\) (mặt phẳng vuông góc với đường sức điện trường là mặt đẳng thế).
Ta có: \(U_{BC}=V_B-V_C=V_B-V_A+V_A-V_C=-U_{AB}+U_{AC}=U_{AC}\)
Mặt khác: \(U_{AC}=U_{CA}=-E.CA=-5000.0,04=-200V\)
b/ Công của lực điện trường khi một êlectron di chuyển từ A đến D:
\(A=-e.U_{AD}\)
với \(U_{AD}=-U_{DA}=-E.DA=-5000.0,02=-100V\)
Vậy \(A=1,6.10^{-19}.\left(-100\right)=1,6.10^{-17}J\)

a. Điện thế tại O: V O = k q 1 A O + k q 2 B O + k q 3 C O
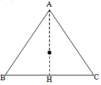
Với A O = A B = C O = 2 3 A H = a 3 3 = 0 , 1 3
→ V O = k A O q 1 + q 2 + q 3 = 1558 , 8 ( V )
b. Điện thế tại H: V H = k q 1 A H + k q 2 B H + k q 3 C H → A H = a 3 2 = 0 , 1 3 2 ; BH = CH = a 2 = 0 , 05
Vậy V H = 658 , 8 ( V )
c. Công của lực điện trường: Electron di chuyển trong vùng điện trường của ba điện tích q 1 , q 2 , q 3 có công không phụ thuộc vào hình dạng đường đi, và bằng độ giảm thế năng điện tích tại điểm đầu và điểm cuối: A = q ( V O − V H ) = − 1 , 6.10 − 19 ( 1558 , 8 − 658 , 8 ) = − 1440.10 − 19 ( J )
d. Công cần thiết để electron di chuyển từ O đến H:
Vì công của lực điện trường trên đoạn OH là A < 0, công cản. Nên công cần thiết để electron di chuyển từ O đến H là: A ’ = - A = 1440 . 10 - 19 J

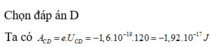
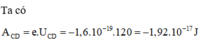
a) Công của lực điện trường di chuyển proton:
b) Công của lực điện trường di chuyển e: