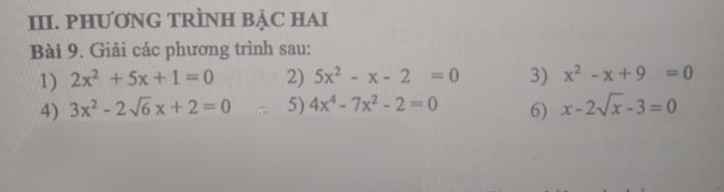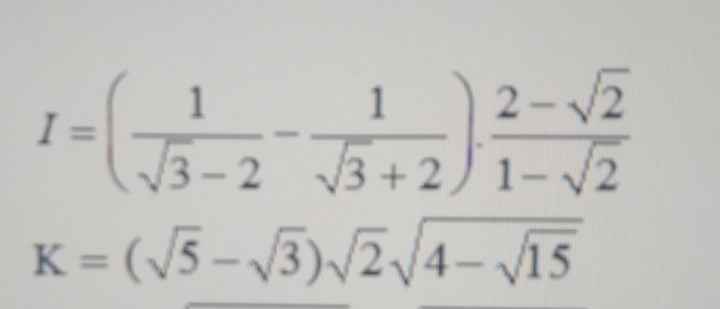Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(\left\{{}\begin{matrix}a-b=x\\b-c=y\\c-a=z\end{matrix}\right.\)thì \(x+y+z=0\).Ngoài ra còn suy ra được:
\(\left\{{}\begin{matrix}x+y=-z\\y+z-x\\x+z=-y\end{matrix}\right.\)
Xét \(A=x^4+y^4+z^4\)
Khai triển Newton để có được :
\(\left(x+y+z\right)^4=\sum x^4+4\sum xy\left(x^2+y^2\right)+12xyz\left(x+y+z\right)+6\sum x^2y^2\)
Vì x+y+z=0 nên \(\sum x^4=x^4+y^4+z^4=-4\sum xy\left(x^2+y^2\right)-6\sum x^2y^2\)
Mà \(-4\sum xy\left(x^2+y^2\right)=-4\sum xy\left[\left(x+y\right)^2-2xy\right]=-4\sum xyz^2+8\sum x^2y^2\)(*)
\(\Rightarrow x^4+y^4+z^4=2\sum x^2y^2-4\sum xyz^2\)
\(=2\left(x^2y^2+y^2z^2+z^2x^2-2xyz^2-2xy^2z-2x^2yz\right)\)
( hm ,có biến ? )
Thực ra từ chỗ (*) thì z ( hoặc x hay y) chưa biết dương hay âm nên có thể đổi thành - z2
Khi đó \(A=2\left(xz+yz-xy\right)^2\)
\(\Rightarrow Bt=\sqrt{2A}=2\left|xz+yz-xy\right|\in Q\)
Câu hỏi đặt ra: liệu có luôn biến đổi được như vậy ? trong trường hợp cả 3 số > 0 thì sao ? Câu trả lời là có.Bởi Vì x+y+z=0 nên phải có ít nhất 1 số khác dấu với 2 số còn lại ( hay dựa vào x+y=-z )

\(A=\sqrt{x}\left(\sqrt{x}-1\right)=x-\sqrt{x}=x-2.\dfrac{1}{2}\sqrt{x}+\dfrac{1}{4}-\dfrac{1}{4}=\left(\sqrt{x}-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\left(x\ge0\right)\)
\(\Rightarrow A_{Min}=-\dfrac{1}{4}."="\Leftrightarrow x=\dfrac{1}{4}\left(TM\right)\)

\(\frac{8\sqrt{41}}{\sqrt{45+4\sqrt{41}}+\sqrt{45-4\sqrt{41}}}\)
\(=\frac{8\sqrt{41}}{\sqrt{41+2.2.\sqrt{41}+4}+\sqrt{41-2.2.\sqrt{4}+4}}\)
\(=\frac{8\sqrt{41}}{\sqrt{\left(\sqrt{41}+2\right)^2}+\sqrt{\left(\sqrt{41}-2\right)^2}}\)
\(=\frac{8\sqrt{41}}{\sqrt{41}+2+\sqrt{41}-2}\)
\(=\frac{8\sqrt{41}}{2\sqrt{41}}=4\)

\(1,\Delta=b^2-4ac=5^2-4.2=17>0\)
=> Pt có 2n pb
\(x_1=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{-5+\sqrt{17}}{4}\)
\(x_2=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{-5-\sqrt{17}}{4}\)


a: Để (d)//y=x-3 thì \(4-m^2=1\)
\(\Leftrightarrow m\in\left\{\sqrt{3};-\sqrt{3}\right\}\)

Bài 27:
a. $4=2.2=2.\sqrt{4}>2.\sqrt{3}$
b. $-\sqrt{5}< -\sqrt{4}=-2$
Bài 28:
a.
\((\sqrt{2}+\sqrt{3})^2=5+2\sqrt{6}=5+2\sqrt{\frac{24}{4}}< 5+2\sqrt{\frac{25}{4}}=5+2.\frac{5}{2}=10\)
$\Rightarrow \sqrt{2}+\sqrt{3}< \sqrt{10}$
b.
\((\sqrt{3}+2)^2=7+4\sqrt{3}\)
\((\sqrt{2}+\sqrt{6})^2=8+4\sqrt{3}\)
Mà $7+4\sqrt{3}< 8+4\sqrt{3}$
$\Rightarrow (\sqrt{3}+2)^2< (\sqrt{2}+\sqrt{6})^2$
$\Rightarrow \sqrt{3}+2< \sqrt{2}+\sqrt{6}$
c.
$\sqrt{15}.\sqrt{17}=\sqrt{15.17}=\sqrt{(16-1)(16+1)}=\sqrt{16^2-1}$
$<\sqrt{16^2}=16$
d.
\((\sqrt{15}+\sqrt{17})^2=32+2\sqrt{15.17}< 32+2.16=64\) (theo kq phần c)
$\Rightarrow \sqrt{15}+\sqrt{17}< \sqrt{64}=8$


\(K=\left(\sqrt{5}-\sqrt{3}\right)\cdot\sqrt{2}\cdot\sqrt{4-\sqrt{15}}\)
\(=\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\)
\(=8-2\sqrt{15}\)
 help,tks mn nhiều <(")
help,tks mn nhiều <(")