K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
29 tháng 11 2023
a: \(\left(9-4\sqrt{5}\right)\left(4\sqrt{5}+9\right)\)
\(=9^2-\left(4\sqrt{5}\right)^2\)
=81-80
=1
b: \(A=\left(\dfrac{\sqrt{x}+1}{x-4}-\dfrac{\sqrt{x}-1}{x+4\sqrt{x}+4}\right)\cdot\dfrac{x\sqrt{x}+2x-4\sqrt{x}-8}{\sqrt{x}}\)
\(=\left(\dfrac{\sqrt{x}+1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}-\dfrac{\sqrt{x}-1}{\left(\sqrt{x}+2\right)^2}\right)\cdot\dfrac{x\left(\sqrt{x}+2\right)-4\left(\sqrt{x}+2\right)}{\sqrt{x}}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)-\left(\sqrt{x}-1\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)^2}\cdot\dfrac{\left(\sqrt{x}+2\right)\left(x-4\right)}{\sqrt{x}}\)
\(=\dfrac{x+3\sqrt{x}+2-x+3\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{x-4}{\sqrt{x}}\)
\(=\dfrac{6\sqrt{x}}{\sqrt{x}}=6\)
9 tháng 4 2022
a: \(-3x^2-8x+3=0\)
\(\Leftrightarrow3x^2+8x-3=0\)
\(\Leftrightarrow3x^2+9x-x-3=0\)
=>(x+3)(3x-1)=0
=>x=1/3 hoặc x=-3
b: \(\left\{{}\begin{matrix}2x+3y=4\\x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+3y=4\\2x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-6\\x=11\end{matrix}\right.\)
15 tháng 8 2019
\(\frac{1}{a}-1=\frac{a+b+c}{a}-\frac{a}{a}=\frac{b+c}{a}\)
Tương tự : \(\frac{1}{b}-1=\frac{c+a}{b};\frac{1}{c}-1=\frac{a+b}{c}\)
Nhân theo vế ta đc :
\(VT=\frac{\left(a+b\right)\left(b+c\right)\left(c+a\right)}{abc}\)
Áp dụng bđt Cauchy :
\(VT\ge\frac{8abc}{abc}=8\)
Dấu "=" xảy ra \(\Leftrightarrow a=b=c=\frac{1}{3}\)
help
20 tháng 6 2021
`d)D=1/2sqrt{a^10b^8}`
`=1/2sqrt{(a^5b^4)^2}`
`=1/2|a^5b^4|`
`=1/2b^4|a^5|`
`a>=0=>D=1/2b^4a^5`
`a<=0=>D=-1/2b^4a^5`
`e)sqrt{(2-sqrt3)^2}+sqrt2`
`=2-sqrt3+sqrt2``
`f)3sqrt5-sqrt{(1-sqrt5)^2}`
`=3sqrt5-(sqrt5-1)`
`=2sqrt5+1`
AT
18 tháng 6 2021
a) Ta có: \(\angle LDI+\angle LBI=90+90=180\Rightarrow LDIB\) nội tiếp
\(\Rightarrow\angle DIL=\angle DBL=\angle DBC=45\) mà \(\Delta IDL\) vuông tại D
\(\Rightarrow\Delta DIL\) vuông cân tại D
b) Ta có: \(\dfrac{1}{DL^2}+\dfrac{1}{DK^2}=\dfrac{1}{DC^2}\) (hệ thức lượng trong tam giác LDK)
mà \(\Delta DIL\) vuông cân tại D \(\Rightarrow DL=DI\Rightarrow\dfrac{1}{DI^2}+\dfrac{1}{DK^2}=\dfrac{1}{DC^2}\)
mà CD là cố định \(\Rightarrow\) đpcm
TA
15 tháng 6 2021
`\sqrt((2a)/3) . \sqrt((3a)/8)`
`= \sqrt((2a)/3 . (3a)/8)`
`= \sqrt((6a^2)/24)`
`=(a\sqrt6)/(2\sqrt6)`
`=1/2 a`
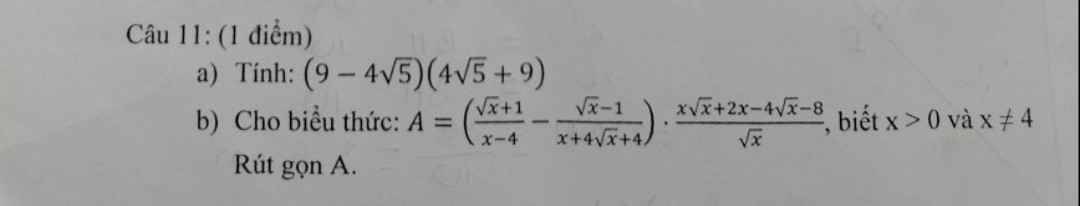
Đặt x+y=a; x-y=b
Hệ \(\Leftrightarrow\left\{{}\begin{matrix}3a-2b=9\\2a+b=-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a-2b=9\\4a+2b=-2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3a-2b=9\\7a=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}3-2b=9\\a=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=-3\\a=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-y=-3\\x+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=-2\\x+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\-1+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x+5y=9\\3x+y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+5y=9\\15x+5y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=-14\\y=\dfrac{9-x}{5}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=2\end{matrix}\right.\)