
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{2x^2+x+9}+\sqrt{2x^2-x+1}=x+4\)
\(\Leftrightarrow\sqrt{2x^2+x+9}-\left(\frac{1}{2}x+3\right)+\sqrt{2x^2-x+1}-\left(\frac{1}{2}x+1\right)=0\)
\(\Leftrightarrow\frac{2x^2+x+9-\left(\frac{1}{2}x+3\right)^2}{\sqrt{2x^2+x+9}+\frac{1}{2}x+3}+\frac{2x^2-x+1-\left(\frac{1}{2}x+1\right)^2}{\sqrt{2x^2-x+1}+\frac{1}{2}x+1}=0\)
\(\Leftrightarrow\frac{\frac{1}{4}x\left(7x-8\right)}{\sqrt{2x^2+x+9}+\frac{1}{2}x+3}+\frac{\frac{1}{4}x\left(7x-8\right)}{\sqrt{2x^2-x+1}+\frac{1}{2}x+1}=0\)
\(\Leftrightarrow\frac{1}{4}x\left(7x-8\right)\left(\frac{1}{\sqrt{2x^2+x+9}+\frac{1}{2}x+3}+\frac{1}{\sqrt{2x^2-x+1}+\frac{1}{2}x+1}\right)=0\)
Dễ thấy: \(\frac{1}{\sqrt{2x^2+x+9}+\frac{1}{2}x+3}+\frac{1}{\sqrt{2x^2-x+1}+\frac{1}{2}x+1}>0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\7x-8=0\end{cases}}\)\(\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{8}{7}\end{cases}}\)
ĐKXĐ:....
Đặt \(\sqrt{2x^2+x+9}=a;\sqrt{2x^2-x+1}=b\)\(\left(a,b>0\right)\)
\(\Rightarrow a^2-b^2=2x^2+x+9-2x^2+x-1=2x+8=2\left(x+4\right)\)
Từ pt ta có:
\(a+b=\dfrac{a^2-b^2}{2}\)\(\Leftrightarrow2\left(a+b\right)=\left(a-b\right)\left(a+b\right)\)
\(\Leftrightarrow\left(a+b\right)\left(a-b-2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a+b=0\left(loại\right)\\a-b-2=0\end{matrix}\right.\)\(\Leftrightarrow a-b=2\)
\(\Leftrightarrow\sqrt{2x^2+x+9}-\sqrt{2x^2-x+1}=2\)
Đến đoạn này giải bằng phương pháp bình phương cả 2 vế, tìm được các giá trị, đối chiếu xem thoả mãn ĐKXĐ không và kết luận tập nghiệm.

a: \(A=\sqrt{3}+1-\sqrt{3}+1=2\)
\(B=\dfrac{x+4\sqrt{x}+4-3\sqrt{x}+6-12}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}=\dfrac{\sqrt{x}-1}{\sqrt{x}-2}\)
b: Để A>2B thì A-2B>0
=>\(\dfrac{2\sqrt{x}-4-\sqrt{x}+1}{\sqrt{x}-2}>0\)
\(\Leftrightarrow\dfrac{\sqrt{x}-3}{\sqrt{x}-2}>0\)
=>x>9 hoặc 0<=x<4

Gọi số tự nhiên cần tìm là \(\overline{ab}\) ( 0< a; b< 9)
=> Sau khi đổi chỗ ta có số: \(\overline{ba}\)
Theo bài ra ta có: \(\overline{ba}-\overline{ab}=45\)
<=> b.10 + a - a.10 -b = 45
<=> 9 ( b - a ) = 45
<=> b - a = 5
+) a = 1 => b = 6
+) a = 2 => b = 7
+) a = 3 => b = 8
+) a = 4 => b = 9
+) a >4 => b >9 loại
Vậy:...

\(3,Đk:x\ge0\\ PT\Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=2\\\sqrt{x}=\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\left(tm\right)\\x=\dfrac{1}{4}\left(tm\right)\end{matrix}\right.\\ 7,ĐK:x\ge0\\ PT\Leftrightarrow\left(\sqrt{x+1}-\sqrt{x\left(x+1\right)}\right)+\left(\sqrt{x}-1\right)=0\\ \Leftrightarrow-\sqrt{x+1}\left(\sqrt{x}-1\right)+\left(\sqrt{x}-1\right)=0\\ \Leftrightarrow\left(\sqrt{x}-1\right)\left(1-\sqrt{x+1}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x+1=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=0\end{matrix}\right.\)
\(4,ĐK:1\le x\le\sqrt{5}\\ PT\Leftrightarrow5-x^2=x^2-2x+1\\ \Leftrightarrow x=-2\left(ktm\right)\Leftrightarrow x\in\varnothing\)

a: \(BC=\sqrt{21^2+72^2}=75\left(cm\right)\)
b: \(AH=\dfrac{21\cdot72}{75}=20.16\left(cm\right)\)
\(BH=\sqrt{21^2-20.16^2}=5.88\left(cm\right)\)
a, Áp dụng PTG: \(BC=\sqrt{AB^2+AC^2}=75\left(cm\right)\)
b, Áp dụng HTL: \(\left\{{}\begin{matrix}BH=\dfrac{AB^2}{BC}=5,88\left(cm\right)\\AH=\dfrac{AB\cdot AC}{BC}=20,16\left(cm\right)\end{matrix}\right.\)
c, Vì BD là p/g nên \(\dfrac{AD}{DH}=\dfrac{AB}{BH}=\dfrac{25}{7}\Rightarrow AD=\dfrac{25}{7}DH\)
Mà \(AD+DH=AH\Rightarrow\dfrac{32}{7}DH=20,16\Rightarrow DH=4,41\left(cm\right)\)
\(\Rightarrow AD=15,75\left(cm\right)\)

hàm số \(y=\left(2m-1\right)x-3m+5\)(d)
a,để (d) cắt trục tung tại điểm có tung độ=-1<=>y=-1
=>-3m+5=-1<=>m=2
b, với m=2 tìm đc ởi ý a=> đồ thị: \(y=3x-1\)
*Cho x=0=>y=-1 ta được A(0;-1)
*Cho y=5=>x=2 ta được B(2;5)
hình vẽ: hơi xấu
c,gọi điểm cố định ấy là C (\(x0;y0\)) thỏa mãn (d)
=>\(y0=\left(2m-1\right)x0-3m+5\)
\(< =>2m.x0-x0-3m+5-y0=0\)
\(< =>2m.x0-3m-x0-y0+5=0\)
\(< =>m\left(2.x0-3\right)+5-x0-y0=0\left(\forall m\right)\)(\(\forall m\))
=>\(\left\{{}\begin{matrix}2x0-3=0\\5-x0-y0=0\end{matrix}\right.< =>\left\{{}\begin{matrix}x0=1,5\\y0=3,5\end{matrix}\right.\)
vậy (d) luon đi qua điểm cố định C(1,5;3,5)

\(S=\dfrac{\Pi\cdot R^2\cdot n}{360}=\dfrac{\Pi\cdot\dfrac{16}{\Pi}\cdot90}{360}=\dfrac{16}{4}=4\)
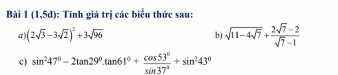
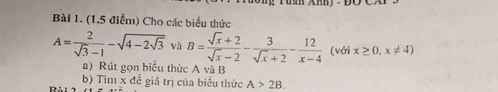



b: \(\sqrt{11-4\sqrt{7}}+\dfrac{2\sqrt{7}-2}{\sqrt{7}-1}\)
\(=\sqrt{7}-2+2\)
\(=\sqrt{7}\)