
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT Bunhiacopxki (cho tất cả các bài):
1.
\(\left(3x+4y\right)^2\le\left(3^2+4^2\right)\left(x^2+y^2\right)=25\)
\(\Rightarrow\left|3x+4y\right|\le5\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{3}{5};\dfrac{4}{5}\right)\)
2.
\(\left(x+2y\right)^2=\left(1.x+\sqrt{2}.\sqrt{2y}\right)^2\le\left(1+2\right)\left(x^2+2y^2\right)=3\)
\(\Rightarrow\left|x+2y\right|\le\sqrt{3}\)
Dấu "=" xảy ra khi \(\left(x;y\right)=\left(\dfrac{1}{\sqrt{3}};\dfrac{1}{\sqrt{3}}\right)\)
4.
a.
Áp dụng Bunhiacopxki:
\(\left(b+c+c+a+a+b\right)\left(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow2\left(a+b+c\right)\left(\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\right)\ge\left(a+b+c\right)^2\)
\(\Rightarrow\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\ge\dfrac{a+b+c}{2}\)
Dấu "=" xảy ra khi \(a=b=c\)


Gọi tọa độ của M là: \(M_{\left(x;y\right)}\)
Ta có: \(\left\{{}\begin{matrix}\overrightarrow{MA}_{\left(-2-x;4-y\right)}\\\overrightarrow{MB}_{\left(1-x;-y\right)}\\3\overrightarrow{MC}_{\left(9-3x;-6-3y\right)}\end{matrix}\right.\)
\(\overrightarrow{MA}+\overrightarrow{MB}=3\overrightarrow{MC}\)
Ta lại có: \(\left(\overrightarrow{MA}+\overrightarrow{MB}\right)_{\left(-1-2x;4-2y\right)}\)
Suy ra: \(\left\{{}\begin{matrix}-1-2x=9-3x\\4-2y=-6-3y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=-10\end{matrix}\right.\)
Vậy tọa độ điểm M là: \(M_{\left(10;-10\right)}\)

tích vô hướng của 2 vecto AB và AC = tích độ dài . Cos góc xen giữa:
= 5 . 5 cos(120) = -25/2
Ngủ đi bạn

1.
\(x^3-mx^2+\left(m-2\right)x+1=0\)
\(\Leftrightarrow x^3-2x+1-m\left(x^2-x\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2+x-1\right)-mx\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^2-\left(m-1\right)x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x^2-\left(m-1\right)x-1=0\left(1\right)\end{matrix}\right.\)
Để pt có 3 nghiệm pb \(\Leftrightarrow f\left(x\right)=x^2-\left(m-1\right)x-1=0\) có 2 nghiệm pb khác 1
\(\Leftrightarrow f\left(1\right)=1-\left(m-1\right)-1\ne0\) (pt trên hiển nhiên luôn có 2 nghiệm pb trái dấu do \(ac=-1< 0\))
\(\Leftrightarrow m\ne1\)
2.
\(x^3+\left(m+1\right)x^2+2mx+4=0\)
\(\Leftrightarrow x^3+x^2+4+mx\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2-x+2\right)+mx\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(x^2+\left(m-1\right)x+2\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x^2+\left(m-1\right)x+2=0\left(1\right)\end{matrix}\right.\)
Pt có 2 nghiệm khi:
TH1: (1) có nghiệm kép khác 2
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-1\right)^2-8=0\\-\dfrac{b}{2a}=\dfrac{1-m}{2}\ne2\end{matrix}\right.\) \(\Rightarrow m=1\pm2\sqrt{2}\)
TH2: (1) có 2 nghiệm pb và 1 nghiệm trong đó bằng 2
\(\Rightarrow\left\{{}\begin{matrix}\Delta=\left(m-1\right)^2-8>0\\f\left(2\right)=4+2\left(m-1\right)+2=0\end{matrix}\right.\) \(\Rightarrow m=-2\)


ĐKXĐ: \(x>3\)
\(\Leftrightarrow2x+2\sqrt{x-3}\sqrt{x+3}=\dfrac{4\left(x+3\right)}{\left(x-3\right)^2}\)
\(\Leftrightarrow\left(\sqrt{x+3}+\sqrt{x-3}\right)^2=\dfrac{4\left(x+3\right)}{\left(x-3\right)^2}\)
\(\Leftrightarrow\sqrt{x+3}+\sqrt{x-3}=\dfrac{2\sqrt{x+3}}{x-3}\)
\(\Leftrightarrow\dfrac{3}{\sqrt{x+3}-\sqrt{x-3}}=\dfrac{\sqrt{x+3}}{x-3}\)
\(\Leftrightarrow3x-9=x+3-\sqrt{x^2-9}\)
\(\Leftrightarrow\sqrt{x^2-9}=12-2x\) (\(x\le6\))
\(\Leftrightarrow x^2-9=144-48x+4x^2\)
\(\Leftrightarrow3x^2-48x+153=0\)
\(\Leftrightarrow x=8-\sqrt{13}\)






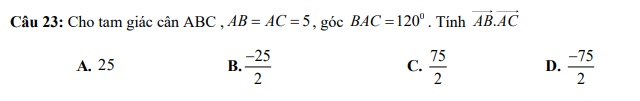
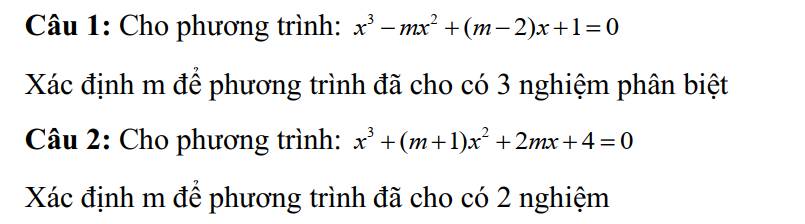 GIÚP MÌNH VỚI! HELP MEEEEEEE 😭
GIÚP MÌNH VỚI! HELP MEEEEEEE 😭

2.A
3.A