
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a: f(x)=0
=>(x-3)(x+3)=0
=>x=3 hoặc x=-3
b: f(x)=0
=>(-2x+4)(2x^2+1)=0
=>4-2x=0
=>x=2

a)\(\frac{a+b}{2}\ge\sqrt{ab}\Rightarrow a+b\ge2\sqrt{ab}\)
\(\Rightarrow a^2+2ab+b^2\ge4ab\)
\(\Rightarrow a^2-2ab+b^2\ge0\Rightarrow\left(a-b\right)^2\ge0\)
Dấu "=" xảy ra khi \(a=b\)
b)Áp dụng BĐT AM-GM ta có:
\(\left\{\begin{matrix}\frac{bc}{a}+\frac{ca}{b}\ge2\sqrt{\frac{bc}{a}\cdot\frac{ca}{b}}=2c\\\frac{bc}{a}+\frac{ab}{c}\ge2\sqrt{\frac{bc}{a}\cdot\frac{ab}{c}}=2b\\\frac{ca}{b}+\frac{ab}{c}\ge2\sqrt{\frac{ca}{b}\cdot\frac{ab}{c}}=2a\end{matrix}\right.\)
Cộng từng vế của 3 BĐT trên rồi thu gọn ta được điều cần chứng minh
Dấu "=" xảy ra khi \(a=b=c\)
c)Áp dụng BĐT AM-GM ta có:
\(\frac{3a+5b}{2}\ge\sqrt{3a\cdot5b}\Leftrightarrow\left(3a+5b\right)^2\ge4\cdot15P\)
\(\Leftrightarrow12^2\ge60P\Leftrightarrow P\le\frac{12}{5}\)
Dấu "=" xảy ra khi \(\left\{\begin{matrix}a=2\\b=\frac{6}{5}\end{matrix}\right.\)

![]() = 100√3 và
= 100√3 và ![]() ngược hướng với hướng
ngược hướng với hướng ![]() với E là đỉnh thứ tư của hình bình hành MACB
với E là đỉnh thứ tư của hình bình hành MACB








 Help me !!!!!
Help me !!!!! HELP ME PLEASE!
HELP ME PLEASE!
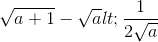 ,a>0
,a>0
help me