
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4b.
\(\dfrac{\pi}{2}< a< \pi\Rightarrow cosa< 0\Rightarrow cosa=-\sqrt{1-sin^2a}=-\dfrac{4}{5}\)
\(\Rightarrow tana=\dfrac{sina}{cosa}=-\dfrac{3}{4}\)
\(tan\left(a+\dfrac{\pi}{3}\right)=\dfrac{tana+tan\left(\dfrac{\pi}{3}\right)}{1-tana.tan\left(\dfrac{\pi}{3}\right)}=\dfrac{-\dfrac{3}{4}+\sqrt{3}}{1-\left(-\dfrac{3}{4}\right).\sqrt{3}}=...\)
c.
\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow cosa>0\Rightarrow cosa=\sqrt{1-sin^2a}=\dfrac{5}{13}\)
\(cos\left(\dfrac{\pi}{3}-a\right)=cos\left(\dfrac{\pi}{3}\right).cosa+sin\left(\dfrac{\pi}{3}\right).sina=\dfrac{1}{2}.\dfrac{5}{13}+\left(-\dfrac{12}{13}\right).\dfrac{\sqrt{3}}{2}=...\)

Lời giải:
Gọi $I(a,b)$ là tâm đường tròn
$(I)$ tiếp xúc với $(d)$ nên: \(R=d(I,(d))=\frac{|a-b+1|}{\sqrt{2}}(*)\)
Mặt khác:
\(\overrightarrow{AB}=(6,-2)\)
\(H(9,4)\) là trung điểm $AB$. \(\overrightarrow{HI}=(a-9,b-4)\)
\(\overrightarrow{HI}\perp \overrightarrow{AB}\Rightarrow 6(a-9)-2(b-4)=0\)
\(\Leftrightarrow 3a-b=23\)
Thay vô $(*)$ thì $R=\frac{|24-2a|}{\sqrt{2}}$
Ta cũng có \(R=IA=\sqrt{(a-6)^2+(b-5)^2}=\sqrt{(a-6)^2+(3a-23-5)^2}\)
\(=\sqrt{10a^2-180a+820}\)
Vậy: \(\frac{|24-2a|}{\sqrt{2}}=\sqrt{10a^2-180a+820}\)
$\Leftrightarrow (24-2a)^2=2(10a^2-180a+820)$
$\Leftrightarrow 16a^2-264a+1064=0$
$\Leftrightarrow 2a^2-33a+133=0$
$\Leftrightarrow a=\frac{19}{2}$ hoặc $a=7$
Đến đây bạn tìm được tâm hình tròn, biết bán kính thì sẽ tìm được pt đường tròn.


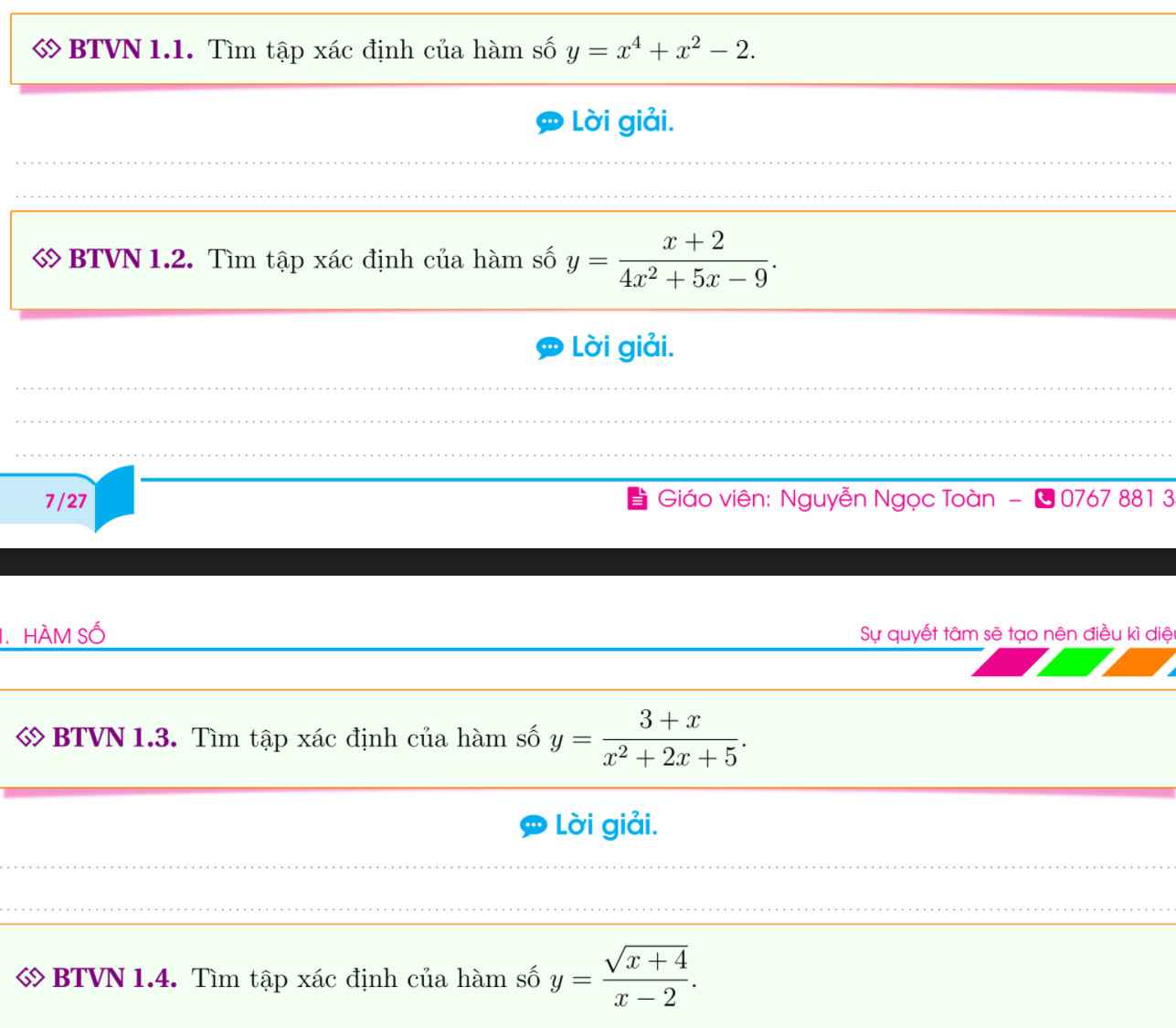
Bài 1.1 TXĐ: $D=\mathbb{R}$
Bài 1.2:
ĐKXĐ: $4x^2+5x-9\neq 0$
$\Leftrightarrow (x-1)(4x+9)\neq 0$
$\Leftrightarrow x\neq 1$ và $x\neq \frac{-9}{4}$
Vậy TXĐ: $D=\mathbb{R}\setminus \left\{1; \frac{-9}{4}\right\}$
Bài 1.3
ĐKXĐ: $x^2+2x+5\neq 0$
$\Leftrightarrow (x+1)^2+4\neq 0$
$\Leftrightarrow (x+1)^2\neq -4\Leftrightarrow x\in\mathbb{R}$
Vậy TXĐ: $D=\mathbb{R}$
Bài 1.4
ĐKXĐ: \(\left\{\begin{matrix} x+4\geq 0\\ x-2\neq 0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq -4\\ x\neq 2\end{matrix}\right.\)
Vậy TXĐ: $D=[-4;+\infty)\setminus \left\{2\right\}$


\(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|4\overrightarrow{MB}-\overrightarrow{MC}\right|\)
⇔ \(\left|2\overrightarrow{MA}+\overrightarrow{MB}\right|=\left|3\overrightarrow{MB}+\overrightarrow{CB}\right|\) (1)
Trên cạnh AB lấy O sao cho \(\dfrac{OA}{OB}=\dfrac{1}{2}\)
⇒ \(2\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{0}\)
Trên cạnh tia đối của tia BC lấy E sao cho \(\dfrac{EB}{BC}=\dfrac{1}{3}\)
⇒ \(3\overrightarrow{EB}+\overrightarrow{CB}=\overrightarrow{0}\)
Vậy (1) ⇒ \(\left|3\overrightarrow{MO}+2\overrightarrow{OA}+\overrightarrow{OB}\right|=\left|3\overrightarrow{ME}+3\overrightarrow{EB}+\overrightarrow{CB}\right|\)
⇒ 3MO = 3ME
⇒ MO = ME
⇒ M nằm trên đường trung trực của OE












Bài 3:
a: Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}4a+b=3\\2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a=4\\2a+b=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=-1-2a=-5\end{matrix}\right.\)