
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a,=\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\sqrt{8-2\sqrt{15}}\\ =\left(4+\sqrt{15}\right)\left(\sqrt{5}-\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)\\ =\left(4+\sqrt{15}\right)\left(8-2\sqrt{15}\right)\\ =32-8\sqrt{15}+8\sqrt{15}-30=2\\ b,=\sqrt{\left(3-\sqrt{5}\right)\left(3+\sqrt{5}\right)}\left(\sqrt{3-\sqrt{5}}+\sqrt{3+\sqrt{5}}\right)\\ =\sqrt{4}\left(\sqrt{\dfrac{5}{2}}-\sqrt{\dfrac{1}{2}}+\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{1}{2}}\right)\\ =2\cdot2\sqrt{\dfrac{5}{2}}=4\sqrt{\dfrac{5}{2}}=2\sqrt{10}\\ c,=\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{1}{2}}-\sqrt{\dfrac{5}{2}}+\sqrt{\dfrac{1}{2}}-\sqrt{2}=2\sqrt{\dfrac{1}{2}}-\sqrt{2}=\sqrt{2}-\sqrt{2}=0\)
\(d,=\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{1}{2}}-\sqrt{\dfrac{7}{2}}-\sqrt{\dfrac{1}{2}}+\sqrt{7}\\ =-2\sqrt{\dfrac{1}{2}}+\sqrt{7}=\sqrt{7}-\sqrt{2}\)
\(e,=\sqrt{6}+\sqrt{\dfrac{1}{2}}+\sqrt{6}-\sqrt{\dfrac{1}{2}}+2\sqrt{6}=4\sqrt{6}\)

Bài 3:
Vì (d') và (d'') cắt nhau tại một điểm trên trục tung nên ta có:
\(\left\{{}\begin{matrix}m+2< >2\\-m^2+4m-2=m-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< >0\\-m^2+3m=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m< >0\\m\left(-m+3\right)=0\end{matrix}\right.\Leftrightarrow m=3\)

\(y\in\left(-\infty;\infty\right)\)
\(-2y^2-3xy-2y+2x^2+6x=1\)
\(-2y^2-3xy-2y-2x^2+6x-1=0\)
\(-2y^2-\left(3x+2\right)y+2x^2+6x-1=0\)
\(y=\frac{\sqrt{25x^2+60x-4-3x-2}}{4}\)
\(y=-\frac{\sqrt{25x^2+60x-4+3x+2}}{4}\)
#Ứng Lân

Lời giải:
\(C=\frac{x+\sqrt{x}+17}{x+\sqrt{x}}=1+\frac{17}{x+\sqrt{x}}\)
Để $C$ nhỏ nhất thì $\frac{17}{x+\sqrt{x}$ nhỏ nhất
Tức là $x+\sqrt{x}$ lớn nhất với mọi $x\geq 0$
Khi $x\geq 0$ thì ta không thể tìm GTLN của $x+\sqrt{x}$ vì cứ cho $x$ tăng vô hạn thì $x+\sqrt{x}$ cũng tăng vô hạn.
Vì vậy biểu thức C không có min bạn nhé. Bạn cần bổ sung thêm điều kiện khác về $x$ để tìm.
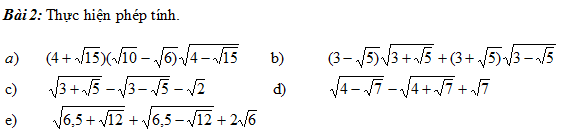
 Help me bài 2 , 3 . Thanks nhiều nhiều ạ
Help me bài 2 , 3 . Thanks nhiều nhiều ạ
xin lỗi nhầm
Ta có: BC^2 = AB^2 + AC^2
= 12^2 + 16^2 = 400
=> BC = √400 = 20 (cm)
Δ ABC vuông có đường cao AH:
=> AB^2 = BH.BC
=> BH = AB^2/BC = 12^2/20 = 7.2 (cm)
=> CH = 20 - 7.2 = 12.8 (cm)
Ta có: AD là phân giác
=> BD/CD = AB/AC
=>( BD + CD)/CD = (AB + AC)/AC
=> 20/CD = 28/16
=> CD = 80/7
=> HD = CH - CD
= 12.8 - (80/7)
= 48/35 (cm)
Bạn tự kẻ hình nhé .
Áp dụng định lý Pytago cho \(\Delta ABC\)vuông tại A ,có :
\(BC=\sqrt{AB^2+AC^2}=\sqrt{12^2+16^2}=\sqrt{400}=20\)
Áp dụng hệ thức lượng trong \(\Delta ABC\)vuông tại A có AH là đường cao ,có :
\(AB^2=BH.BC\)
\(\Rightarrow BH=\frac{AB^2}{BC}=\frac{12^2}{20}=7,2\)
Áp dụng tính chất đường phân giác trong \(\Delta ABC\)có AD là phân giác :
\(\frac{BD}{AB}=\frac{CD}{AC}\Rightarrow\frac{BD}{12}=\frac{CD}{16}\)
\(\Rightarrow\frac{BD}{12}=\frac{CD}{16}=\frac{BD+CD}{12+16}=\frac{BC}{28}=\frac{20}{28}=\frac{5}{7}\)
\(\Rightarrow BD=12.\frac{5}{7}=\frac{60}{7}\)
Ta có : \(BH=7,2< \frac{60}{7}=BD\)
\(\Rightarrow H\)nằm giữa B và D
\(\Rightarrow HD=BD-BH=\frac{60}{7}-7,2=\frac{48}{35}\)
Áp dụng định lí Pytago cho \(\Delta AHD\)vuông tại H ,có:
\(AD=\sqrt{AH^2+HD^2}=\sqrt{\left(7,2\right)^2+\left(\frac{48}{35}\right)^2}\approx7,33\)