
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1. Điền kí hiệu ( ∈,⊂, ∉) thích hợp vào ô vuông
– 3 ∉ N – 3 ∈ Z -3 ∈ Q
-2/3 ∉ Z -2/3 ∈ Q N ⊂ Z ⊂ Q
Bài 2 trang 7. Trong các phân số sau, những phân số nào biểu diễn số hữu tỉ 3/-4

bài 3
hD Giải: a) x= 2/-7 = -22/7;y = -3/11= -21/77
Vì -22 < -21 và 77> 0 nên x <y
b)![]() Vì -216 < -213 và 300 > 0 nên y < x
Vì -216 < -213 và 300 > 0 nên y < x
c) x = -0,75 = -75/100 = -3/4; y = -3/4
Vậy x=y
Bài 4. So sánh số hữu tỉ a/b ( a,b ∈ Z, b # 0) với số 0 khi a, b cùng dấu và khi a, b khác dấu
HD giải: Với a, b ∈ Z, b> 0
– Khi a , b cùng dấu thì a/b > 0
– Khi a,b khác dấu thì a/b < 0
Tổng quát: Số hữu tỉ a/b ( a,b ∈ Z, b # 0) dương nếu a,b cùng dấu, âm nếu a, b khác dấu, bằng 0 nếu a = 0

Bài 5:
Vì \(ab//cd\) và AB cắt ab và cd
Nên \(\widehat{bAB}+\widehat{ABd}=180^0\) (Hai góc trong cùng phía)
Mà Am là tia phân giác của \(\widehat{bAB}\)
\(\Rightarrow\widehat{BAm}=\dfrac{1}{2}.\widehat{bAB}\)
và Bn là tia phân giác của \(\widehat{ABd}\)
\(\Rightarrow\widehat{ABn}=\dfrac{1}{2}.\widehat{ABd}\)
Xét tam giác ABC, có:
\(\widehat{ABC}+\widehat{CAB}+\widehat{ACB}=180^0\)
Hay \(\widehat{ABn}+\widehat{BAm}+\widehat{ACB}=180^0\)
\(\Leftrightarrow\dfrac{1}{2}.\widehat{ABd}+\dfrac{1}{2}.\widehat{BAb}+\widehat{ACB}=180^0\)
\(\Leftrightarrow\dfrac{1}{2}.\left(\widehat{ABd}+\widehat{BAb}\right)+\widehat{ACB}=180^0\)
\(\Leftrightarrow\dfrac{1}{2}.180^0+\widehat{ACB}=180^0\)
\(\Leftrightarrow90^0+\widehat{ACB}=180^0\)
\(\Leftrightarrow\widehat{ACB}=180^0-90^0=90^0\)
Hay \(Am\perp Bn\left(đpcm\right)\)
Chúc bạn học tốt!
Bài 6:
Vì \(AB//CD\)
Nên \(\widehat{ABC}=\widehat{DCB}\) (Hai góc so le trong)
Mà \(\left\{{}\begin{matrix}\widehat{ABC}=x+x\\\widehat{DCB}=120^0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\widehat{ABC}=2x\\\widehat{DCB}=120^0\end{matrix}\right.\)
\(\Leftrightarrow2x=120^0\)
\(\Leftrightarrow x=\dfrac{120^0}{2}=60^0\)
Vậy \(x=60^0\).
Chúc bạn học tốt!

a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.


Sao không viết câu hỏi ra đây luôn đi chứ có thể nhièu người biết mà không có sách lắm! Sao hướng dẫn được

a) | 9 + 7x | = 3 - 5x
\(\Rightarrow\orbr{\begin{cases}9+7x=3-5x\\9+7x=-\left(3-5x\right)\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}7x+5x=3-9\\9+7x=-3+5x\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}12x=-6\\7x-5x=-3-9\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{6}\\2x=-12\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{6}\\x=-6\end{cases}}\)




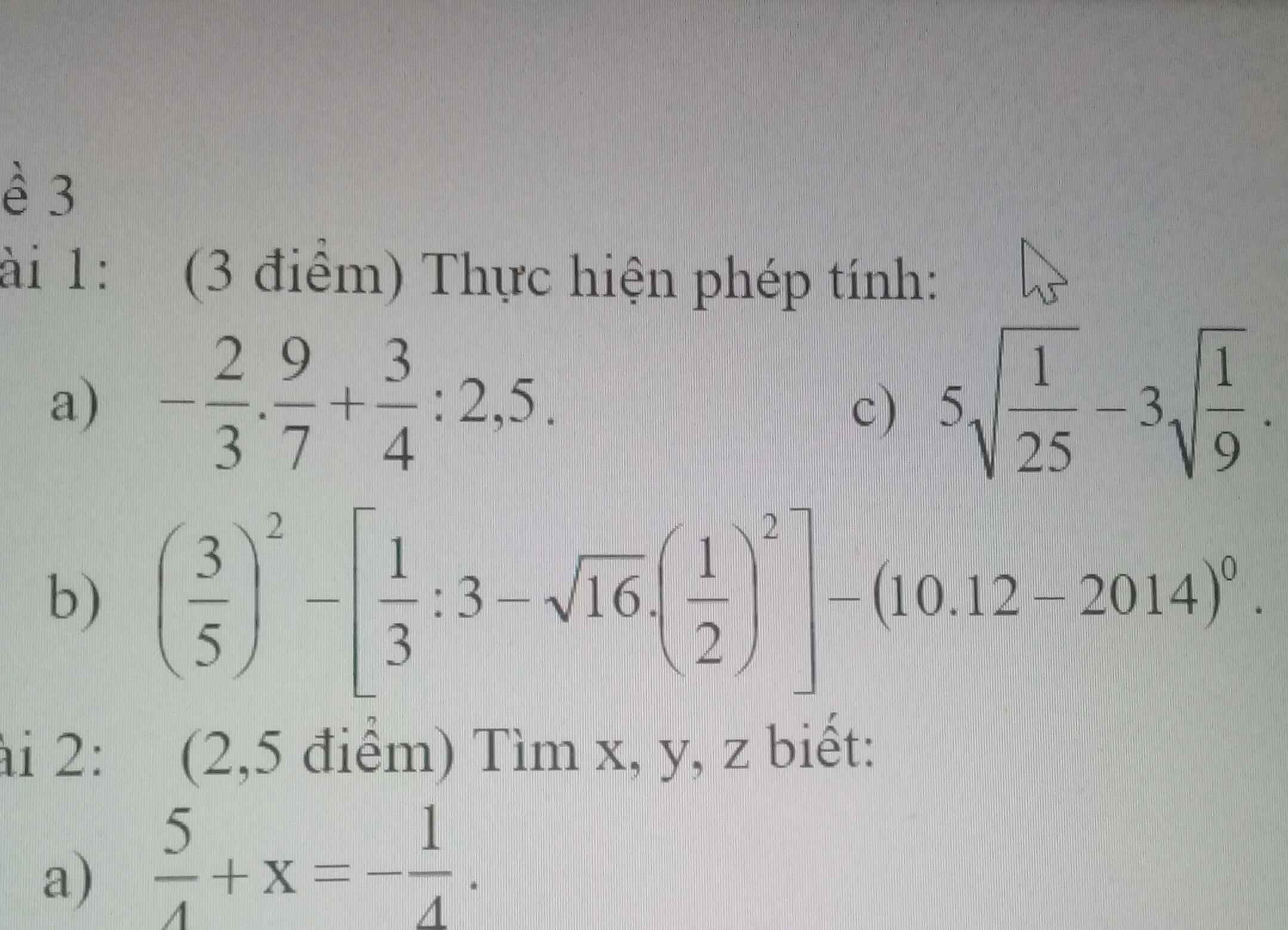


 Ai giúp em đc bài nào thì giúp em vs ạ . Mai em cần rồi nhé !!:))
Ai giúp em đc bài nào thì giúp em vs ạ . Mai em cần rồi nhé !!:))
bài đâu em :V ?