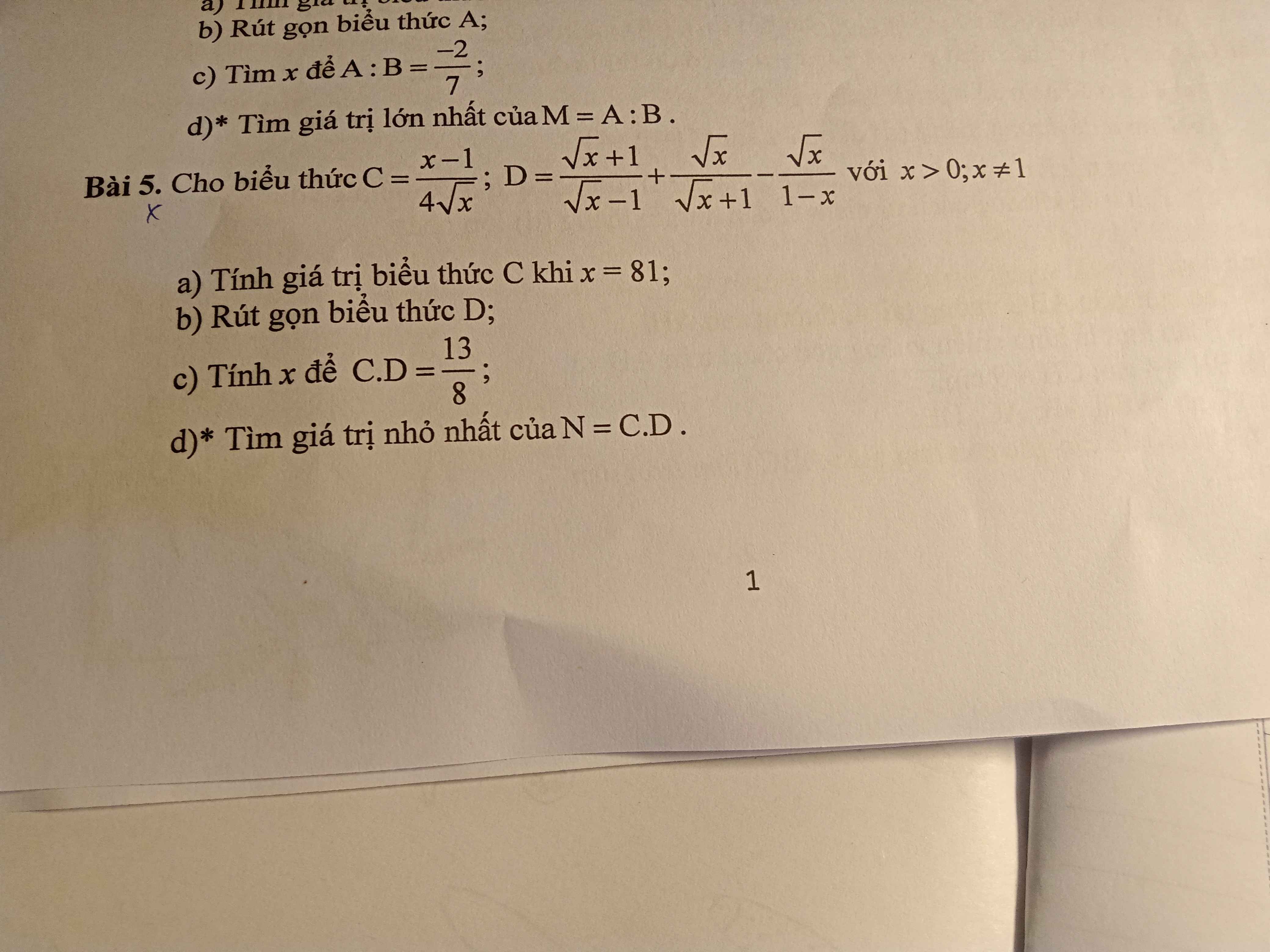K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 6 2023
3:
b: x1^2+x2^2=12
=>(x1+x2)^2-2x1x2=12
=>(2m+2)^2-4m=12
=>4m^2+4m+4=12
=>m^2+m+1=3
=>(m+2)(m-1)=0
=>m=1;m=-2
2:
b: =>|x1|-|x2|=m+3-|-1|=m+2
=>x1^2+x2^2-2|x1x2|=m+2
=>(x1+x2)^2-2x1x2-2|x1x2|=m+2
=>(2m)^2-2(-1)-2|-1|=m+2
=>4m^2-m-2=0
=>m=(1+căn 33)/8; m=(1-căn 33)/8
TT
các cao nhân giúp em vs ạ
1
NV
Nguyễn Việt Lâm
Giáo viên
20 tháng 9 2021
\(P=\dfrac{18}{x}+\dfrac{9}{y}+\dfrac{x}{6}-\dfrac{5y}{12}+2019\)
\(P=\left(\dfrac{x}{2}+\dfrac{18}{x}\right)+\left(\dfrac{y}{4}+\dfrac{9}{y}\right)-\dfrac{1}{3}\left(x+2y\right)+2019\)
\(P\ge2\sqrt{\dfrac{18x}{2x}}+2\sqrt{\dfrac{9y}{4y}}-\dfrac{1}{3}.18+2019=2022\)
Dấu "=" xảy ra khi \(x=y=6\)
18 tháng 12 2021
a: Thay x=81 vào C, ta được:
\(C=\dfrac{81-1}{4\cdot9}=\dfrac{80}{36}=\dfrac{20}{9}\)
ND
1
26 tháng 1 2022
ĐKXĐ a>0 \(a\ne4,a\ne\dfrac{1}{9}\)\(P=\left(\dfrac{a-\sqrt{a}-2\sqrt{a}+2}{3a-6\sqrt{a}-\sqrt{a}+2}-\dfrac{\sqrt{a}-3}{3a-9\sqrt{a}+\sqrt{a}-3}+\dfrac{8\sqrt{a}}{\left(3\sqrt{a}-1\right)\left(3\sqrt{a}+1\right)}\right):\left(\dfrac{a+\sqrt{a}}{3\sqrt{a}+1}\right)\)bạn phân tích thành nhân tử và rút gọn cho mẫu thì nó bằng
\(\left(\dfrac{\sqrt{a}-1}{3\sqrt{a-1}}-\dfrac{1}{3\sqrt{a}+1}+\dfrac{8\sqrt{a}}{\left(3\sqrt{a}-1\right)\left(3\sqrt{a}+1\right)}\right).\dfrac{3\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{3a+3\sqrt{a}}{\left(3\sqrt{a}-1\right)\left(3\sqrt{a}+1\right)}.\dfrac{3\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{3\sqrt{a}\left(\sqrt{a}+1\right)}{\left(3\sqrt{a}+1\right)\left(3\sqrt{a}-1\right)}.\dfrac{3\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}+1\right)}=\dfrac{3}{3\sqrt{a}-1}\)
để P>\(\dfrac{3}{\left|1-3\sqrt{5}\right|}\)thì \(\dfrac{3}{3\sqrt{a}-1}>\dfrac{3}{3\sqrt{5}-1}\)(vì có dấu giá trị tuyệt đối mà có 1<3\(\sqrt{5}\) nên phải đổi dấu khi ra khỏi ngoặc nhé
=>\(\dfrac{1}{3\sqrt{a}-1}>\dfrac{1}{3\sqrt{5}-1}=>3\sqrt{a}-1< 3\sqrt{5}-1< =>\sqrt{a}< \sqrt{5}< =>a< 25\)
mà ngta muốn gtrij nguyên lớn nhất của a vậy a =24
G
8 tháng 8 2023
\(B=\sqrt{\dfrac{a+6}{a+1}}\) ( ĐK: \(a>-1;a\le-6\) )
\(\Rightarrow B^2=\dfrac{a+6}{a+1}=1+\dfrac{5}{a+1}\)
Với \(B\in Z\Rightarrow B^2\in Z\Leftrightarrow\dfrac{5}{a+1}\in Z\)
a) mà \(a\in Z\) nên \(a+1\inƯ\left(5\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}a+1=\pm1\\a+1=\pm5\end{matrix}\right.\)\(\Leftrightarrow a=0\) ,\(a=4\) hoặc \(a=-6\)
Tại \(a=0\Leftrightarrow B=\sqrt{6}\) (loại)
Tại \(a=4\Rightarrow B=\sqrt{2}\) (loại)
Tại \(a=-6\Rightarrow B=0\) (tm)
Vậy \(a=-6\)
b) Thay \(a=\dfrac{4}{9}\Rightarrow B=\dfrac{\sqrt{754}}{13}\)
Hm...
c) Đợi cao nhân. Đề này quá sức của thần.