
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Số cam trong vườn là :
450 . \(\frac{2}{5}\) = 180 ( cây )
Số hồng xiêm trong vườn là :
450 . 50% = 225 ( cây )
Số bưởi trong vườn là :
450 - 180 - 225 = 45 ( cây )
Đ/s : 45 cây bưởi

Công thức
(x-\(\frac{1}{3}\)):\(\frac{-12}{45}\)+1=\(\frac{1}{3}\)
(x-\(\frac{1}{3}\)):\(\frac{-12}{45}\)=\(\frac{1}{3}\)+1
(x-\(\frac{1}{3}\)):\(\frac{-12}{45}\)=\(\frac{4}{3}\)
(x-\(\frac{1}{3}\))=\(\frac{4}{3}\)x\(\frac{-12}{45}\)
(x-\(\frac{1}{3}\))=\(\frac{-16}{45}\)
x=\(\frac{-16}{45}\)+\(\frac{1}{3}\)
x=\(\frac{-1}{45}\)

\(H=\frac{10}{56}+\frac{10}{140}+\frac{10}{260}+...+\frac{10}{1400}\)
\(\Rightarrow H=\frac{5}{28}+\frac{5}{70}+\frac{5}{130}+...+\frac{5}{700}\)
\(\Rightarrow\frac{3H}{5}=\frac{3}{4.7}+\frac{3}{7.10}+\frac{3}{10.13}+...+\frac{3}{25.28}\)
\(\Rightarrow\frac{3H}{5}=\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{10}+\frac{1}{10}-\frac{1}{13}+...+\frac{1}{25}-\frac{1}{28}\)
\(\Rightarrow\frac{3H}{5}=\frac{1}{4}-\frac{1}{28}\)
\(\Rightarrow\frac{3H}{5}=\frac{3}{14}\)
\(\Rightarrow H=\frac{3}{14}.\frac{5}{3}\)
\(\Rightarrow H=\frac{5}{14}\)
Vậy \(H=\frac{5}{14}\)

BÀI 1:
a)
\(\dfrac{1}{2}-\dfrac{2}{3}+\dfrac{3}{4}\\ =\dfrac{6}{12}-\dfrac{8}{12}+\dfrac{9}{12}\\ =\dfrac{6-8+9}{12}\\ =\dfrac{7}{12}\)
b)
\(-4\dfrac{1}{2}+1,2\cdot\left(-5\right)-30\%\\ =\dfrac{-9}{2}+\dfrac{6}{5}\cdot\left(-5\right)-\dfrac{3}{10}\\ =\dfrac{-9}{2}+\left(-6\right)-\dfrac{3}{10}\\ =\dfrac{-45}{10}+\dfrac{-60}{10}-\dfrac{3}{10}\\ =\dfrac{\left(-45\right)+\left(-60\right)-3}{10}\\ =\dfrac{-108}{10}\\ =\dfrac{54}{5}\)
c)
\(\dfrac{-7}{9}\cdot\dfrac{6}{13}+\dfrac{-7}{9}\cdot\dfrac{7}{13}+5\dfrac{7}{9}\\ =\dfrac{-7}{9}\cdot\left(\dfrac{6}{13}+\dfrac{7}{13}\right)+5\dfrac{7}{9}\\ =\dfrac{-7}{9}\cdot1+5\dfrac{7}{9}\\ =\dfrac{-7}{9}+5\dfrac{7}{9}\\ =5\)
BÀI 2
a)
\(\dfrac{3}{2}x-\dfrac{2}{3}=\dfrac{2}{3}:\dfrac{3}{2}\\ \dfrac{3}{2}x-\dfrac{2}{3}=\dfrac{4}{9}\\ \dfrac{3}{2}x=\dfrac{4}{9}+\dfrac{2}{3}\\ \dfrac{3}{2}x=\dfrac{10}{9}\\ x=\dfrac{10}{9}:\dfrac{3}{2}\\ x=\dfrac{20}{27}\)
b)
\(\left(\dfrac{9}{11}-x\right):\left(\dfrac{-10}{11}\right)=1-\dfrac{4}{5}\\ \left(\dfrac{9}{11}-x\right):\left(\dfrac{-10}{11}\right)=\dfrac{1}{5}\\ \dfrac{9}{11}-x=\dfrac{1}{5}\cdot\left(\dfrac{-10}{11}\right)\\ \dfrac{9}{11}-x=\dfrac{-2}{11}\\ x=\dfrac{9}{11}-\dfrac{-2}{11}\\ x=1\)
c)
\(\left(1,2x-\dfrac{4}{7}\right):\dfrac{4}{7}=75\%\\ \left(\dfrac{6}{5}x-\dfrac{4}{7}\right):\dfrac{4}{7}=\dfrac{3}{4}\\ \dfrac{6}{5}x:\dfrac{4}{7}-\dfrac{4}{7}:\dfrac{4}{7}=\dfrac{3}{4}\\ \dfrac{6}{5}x:\dfrac{4}{7}-1=\dfrac{3}{4}\\ \dfrac{6}{5}x:\dfrac{4}{7}=\dfrac{3}{4}+1\\ \dfrac{6}{5}x:\dfrac{4}{7}=\dfrac{7}{4}\\ \dfrac{6}{5}x=\dfrac{7}{4}\cdot\dfrac{4}{7}\\ \dfrac{6}{5}x=1\\ x=1:\dfrac{6}{5}\\ x=\dfrac{5}{6}\)

\(\Rightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Rightarrow\dfrac{5}{4}+\dfrac{2}{5}=\dfrac{3}{10}x-\dfrac{1}{4}x\)
\(\Rightarrow\dfrac{33}{20}=\dfrac{11}{20}x\)
\(\Rightarrow x=\dfrac{33}{20}\div\dfrac{11}{20}\)
\(\Rightarrow x=3\)
\(1\dfrac{1}{4}-x\dfrac{1}{4}=x\cdot30\%\cdot\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-x\dfrac{1}{4}=x\cdot\dfrac{3}{10}-\dfrac{2}{5}\)
\(\Leftrightarrow\dfrac{5}{4}-\dfrac{1}{4}x=\dfrac{3}{10}x-\dfrac{2}{5}\)
\(\Leftrightarrow25-5x=6x-8\)
\(\Leftrightarrow-5x-6x=-8-25\)
\(\Leftrightarrow-11x=-33\)
\(\Leftrightarrow x=3\)
Vậy x = 3

1.
Ta có
Từ 100 đến 199 có 19 số chứa chữ số 7
Từ 200 đến 299 có 19 số chứa chữ số 7
Cứ như vậy đến hết ta tìm được từ 100 đến 999 có số các số chứa chữ số 7 là:
19.8 + 100 = 252 (số)
Có số số có 3 chữ số là:
(999 - 100) : 1 + 1 = 900 (số)
Vậy có số số có 3 chữ số mà trong đó có 1 chữ số 7 là:
900 - 252 = 648 (số)
Đáp số : 648 số
Bài 1: Có 3 dạng:
Dạng 1: \(\overline{7ab}\) , ở dạng này a, b có 9 cách chọn (trừ chữ số 7). Vậy có: 9.9=81 số ở dạng này.
Dạng 2: \(\overline{a7b}\) , ở dạng này a có 8 cách chọn (trừ chữ số 0 và 7), b có 9 cách chọn. Vậy có: 8.9=72 số ở dạng này.
Dạng 3: \(\overline{ab5}\) , ở dạng này a có 8 cách chọn (trừ chữ số 0 và 7), b có 9 cách chọn. Vậy có: 8.9=72 số ở dạng này.
Vậy tổng cộng có: 81+72+72=225 số có 3 chữ số trong đó có đúng một chữ số 7.
Bài 2:Ở bài này có 2 dạng.
\(-\)Nếu a=0 thì với 4 chữ số 3;5;7;0 ta có thể lập được:
Ở hàng nghìn có 3 cách chọn.
Ở hàng trăm có 3 cách chọn.
Ở hàng chục có 2 cách chọn.
Ở hàng đơn vị có 1 cách chọn.
Vậy có:3.3.2=18 số ( loại )
\(-\)Nếu a>0 thì với 4 chữ số 3;5;7;a(a>0) ta có thể lập được:
Ở hàng nghìn có 4 cách chọn.
Ở hàng trăm có 3 cách chọn.
Ở hàng chục có 2 cách chọn.
Ở hàng đơn vị có 1 cách chọn.
Vậy có: 4.3.2=24 số ( loại )
Vậy không tìm được giá trị thoã mãn của a.
Chúc bạn học tốt!!!
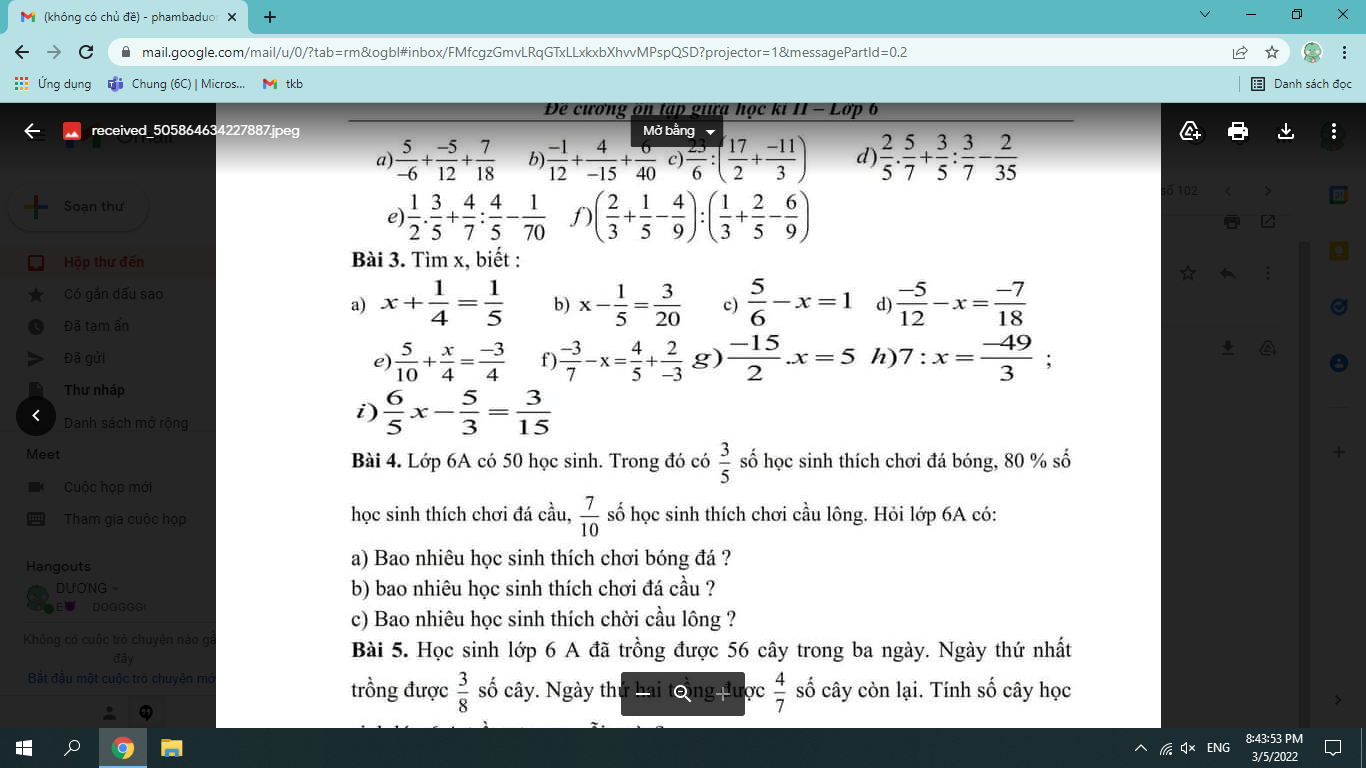 help bài 3 câu a ,b, và c help
help bài 3 câu a ,b, và c help


 HELP ME
HELP ME


 HELP!!!
HELP!!!





a) \(x+\dfrac{1}{4}=\dfrac{1}{5}\)
\(x=\dfrac{1}{5}-\dfrac{1}{4}\)
\(x=\dfrac{4}{20}-\dfrac{5}{20}\)
\(x=-\dfrac{1}{20}\)
b) \(x-\dfrac{1}{5}=\dfrac{3}{20}\)
\(x=\dfrac{3}{20}+\dfrac{1}{5}\)
\(x=\dfrac{3}{20}+\dfrac{4}{20}\)
\(x=\dfrac{7}{20}\)
c) \(\dfrac{5}{6}-x=1\)
\(x=\dfrac{5}{6}-1\)
\(x=\dfrac{5}{6}-\dfrac{6}{6}\)
\(x=-\dfrac{1}{6}\)