Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: \(x^2-5x+3=0\)
Áp dụng định lí viet ta có: \(\hept{\begin{cases}x_1+x_2=5\\x_1x_2=3\end{cases}}\)
a) \(A=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=5^2-2.3=19\)
b) \(B=x_1^3+x_2^3=\left(x_1+x_2\right)^3-3\left(x_1+x_2\right)x_1x_2=5^3-3.5.3=80\)
c) \(C=\left|x_1-x_2\right|\)>0
=> \(C^2=x_1^2+x_2^2-2x_1x_2=19-2.3=13\)
=> C = căn 13
d) \(D=x_2+\frac{1}{x_1}+x_1+\frac{1}{x_2}=\left(x_1+x_2\right)+\frac{x_1+x_2}{x_1x_2}=5+\frac{5}{3}=5\frac{5}{3}\)
e) \(E=\frac{1}{x_1+3}+\frac{1}{x_2+3}=\frac{\left(x_1+x_2\right)+6}{x_1x_2+3\left(x_1+x_2\right)+9}=\frac{5+6}{3+3.5+9}=\frac{11}{27}\)
g) \(G=\frac{x_1-3}{x_1^2}+\frac{x_2-3}{x_2^2}=\left(\frac{1}{x_1}+\frac{1}{x_2}\right)-3\left(\frac{1}{x_1^2}+\frac{1}{x_2^2}\right)\)
\(=\frac{x_1+x_2}{x_1x_2}-3\frac{x_1^2+x_2^2}{x_1^2.x_2^2}=\frac{5}{3}-3.\frac{19}{3^2}=-\frac{14}{3}\)
a)Với y=1 ta có hpt:
\(\int^{2x+3=3+m}_{x+2=m}\Leftrightarrow\int^{2x=m}_{x+2=2x}\Leftrightarrow\int^{2.2=m}_{x=2}\Leftrightarrow\int^{m=4}_{x=2}\)
Vậy nghiệm của hpt là (2;1) khi m=4
b)đợi suy nghĩ
\(Đkxđ:\hept{\begin{cases}x\ge2\\y\ge2\end{cases}}\)
Ta thấy các vế đều \(\ge0\)nên ta bình phương các vế ta được:
\(\Leftrightarrow\hept{\begin{cases}x+y+3+2\sqrt{\left(x+5\right)\left(y-2\right)}=49\\x+y+3+2\sqrt{\left(x-2\right)\left(y+5\right)}=49\end{cases}}\)
Trừ từng vế ta được:
\(\sqrt{\left(x+5\right)\left(y-2\right)}=\sqrt{\left(x-2\right)\left(y+5\right)}\)
\(\Leftrightarrow\left(x+5\right)\left(y-2\right)=\left(x-2\right)\left(y+5\right)\)
\(\Leftrightarrow xy+5y-2x-10=xy+5x-2y-10\)
\(\Leftrightarrow x=y\)
Thay vào một trong hai pt trên ta được:
\(2x+3+2\sqrt{x^2+3x-10}=49\)
\(\Leftrightarrow\sqrt{x^2+3x-10}=23-x\Leftrightarrow\hept{\begin{cases}x\le23\\x^2+3x-10=\left(23-x\right)^2\end{cases}}\Leftrightarrow x=11\)
Vậy hpt có nghiệm là: \(x=y=11\)
pt thứ 1 <=> (x+y)2 - 3xy = 19
Pt thứ 2 <=> x+ y = -7 - xy. Thế vào pt (1) ta được:
(-7 - xy)2 - 3xy = 19
<=> 49 + 14xy + (xy)2 - 3xy = 19
<=> (xy)2 + 11xy + 30 = 0
<=> (xy)2 + 5xy + 6xy + 30 = 0 <=> (xy + 5).(xy + 6) = 0 <=> xy = -5 hoặc xy = -6
+) xy = -5 => x+ y = -2 => x = -2 - y => xy = -(y +2).y = -5 <=> y2 + 2y - 5 = 0 <=> (y+1)2 - 6 = 0
<=> y + 1 = \(\sqrt{6}\) hoặc y + 1 = - \(\sqrt{6}\)
=> y = \(\sqrt{6}\) - 1 ; x = -1 - \(\sqrt{6}\)
y = - \(\sqrt{6}\) -1 => x = -1 + \(\sqrt{6}\)
+) xy = -6 => x + y = -1 => x = -y - 1 => xy = -(y+1).y = -6 => y2 + y - 6 = 0 <=> y2 + 3y - 2y - 6 = 0
<=> (y - 2)(y +3) = 0 <=> y = 2 hoặc y = -3
Với y = 2 => x = -3
với y = -3 => x = 2
Vậy hệ có 4 nghiệm....
từ ptt 2
=>x=4-my
thay vào pt 1 ta đc:
m(4-my)+4y=10-m
=>4m-m^2y+4y=10-m
=> m^2y-4y+10-5m=0
no duy nhất x,y nên pt trên cs 1 no
=> đenta phẩy =0
=> 4-y(-5m)=0
5+5ym=0
=>ym=0
=>y=0
vậy đpcm
ak nhầm,
m^2y-4y+10-5m=0
=> denta =25-4y(-4y+10)=0
=>25+16y^2-40y=0
=>16y^2-40y+ 25=0
y=1.25
=> đpcm
vô lý
3, y nhỏ nhất khi y^2 nhỏ nhất
y^2 = \(x+2\sqrt{x-1}+x-2\sqrt{x-1}+2\sqrt{\left(x-2\sqrt{x-1}\right)\left(x+2\sqrt{x-1}\right)}\)
= \(2x+2\sqrt{x^2-4x+4}=2x+2\sqrt{\left(x-2\right)^2}=2x+2!x-2!\)
(Đến đây thì chịu rồi)
A^2 = \(2+\frac{\sqrt{7}}{2}+2-\frac{\sqrt{7}}{2}-2\sqrt{\left(2+\frac{\sqrt{7}}{2}\right)\left(2-\frac{\sqrt{7}}{2}\right)}\)
A^2 = \(4\) \(-2\sqrt{4-\frac{7}{4}}=\) \(4-2\sqrt{\frac{9}{4}}=4-2\cdot\frac{3}{2}=4-3=1\)
=> A = 1
1.
a.\(\Delta=\left(4m+1\right)^2-8\left(m-4\right)=16m^2+33>0\left(\forall m\in R\right)\)
b.Gia su 2 nghiem cua PT la \(x_1,x_2\left(x_1>x_2\right)\)
Theo de bai ta co;\(x_1-x_2=17\)
Tu cau a ta co:\(x_1=\frac{-4m-1+\sqrt{16m^2+33}}{2}\) \(x_2=\frac{-4m-1-\sqrt{16m^2+33}}{2}\)
\(\Rightarrow\frac{-4m-1+\sqrt{16m^2+33}}{2}-\frac{-4m-1-\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow\frac{2\sqrt{16m^2+33}}{2}=17\)
\(\Leftrightarrow16m^2+33=289\)
\(\Leftrightarrow m=4\)
2.
a.\(\Delta'=\left(m-1\right)^2-\left(m+2\right)\left(3-m\right)=2m^2-3m-5=\left(m+1\right)\left(2m-5\right)>0\)
TH1:\(\hept{\begin{cases}m+1>0\\2m-5>0\end{cases}\Leftrightarrow m>\frac{5}{2}}\)
TH2:\(\hept{\begin{cases}m+1< 0\\2m-5< 0\end{cases}\Leftrightarrow m< -1}\)
Xet TH1:\(x_1=\frac{-m+1+\sqrt{2m^2-3m-5}}{m+2}\) \(x_2=\frac{-m+1-\sqrt{2m^2-3m-5}}{m+2}\)
Ta co:\(x^2_1+x^2_2=x_1+x_2\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1.x_2=x_1+x_2\)
\(\Leftrightarrow\left(\frac{-2m+2}{m+2}\right)^2-\frac{-m^2+5m+6}{\left(m+2\right)^2}=\frac{-2m+2}{m+2}\)
\(\Leftrightarrow\frac{5m^2-13m-2}{\left(m+2\right)^2}=\frac{-2m^2-2m+4}{\left(m+2\right)^2}\)
\(\Rightarrow7m^2-11m-6=0\)
\(\Delta_m=121+168=289>0\)
\(\Rightarrow\hept{\begin{cases}m_1=2\left(l\right)\\m_2=-\frac{3}{7}\left(l\right)\end{cases}}\)
TH2;Tuong tu
Vay khong co gia tri nao cua m de PT co 2 nghiem thoa man \(x^2_1+x^2_2=x_1+x_2\)
Chọn đáp án B
⇒ Hệ phương trình đã cho vô nghiệm ⇒ S = ∅
Cách 2: Ta thấy: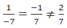
⇒ Hệ pt vô nghiệm