Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Điều kiện để xuất hiện sóng dừng trên dây có hai đầu cố định là L = \(n\frac{\lambda }{2}\)
Từ hình vẽ ta thấy trên dây xuất hiện 3 bụng sóng ⇒ n = 3
⇒ λ=\(\frac{{2L}}{n}\) = \(\frac{{2.1,2}}{3}\)= 0,8 (m)
Tốc độ sóng truyền trên dây là: v = λf = 0,8.13,3 = 10,64 (m/s)

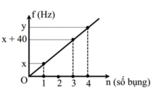
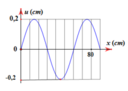
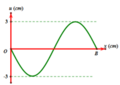
a. Dựa vào đồ thị ta có:
Chu kì \(T = 2 s\), suy ra tần số góc \(\omega = \frac{2 \pi}{T} = \frac{2 \pi}{2} = \pi\) rad/s
Vận tốc cực đại của dao động: \(\text{v}_{m a x} = \omega A\)
\(\Rightarrow A = \frac{\text{v}_{m a x}}{\omega} = \frac{4}{\pi}\) cm
Thời điểm \(t = 0\), vật có \(\text{v} = \text{v}_{m a x}\), suy ra vật ở VTCB và \(\text{v} > 0\)
Khi đó: \(x = 0 \Rightarrow cos \varphi = 0 \Rightarrow \varphi = - \frac{\pi}{2}\)
Phương trình của vận tốc có dạng: \(\text{v} = \omega A cos \left(\right. \omega t + \varphi + \frac{\pi}{2} \left.\right)\)
\(\Rightarrow \text{v} = 4 cos \left(\right. \pi t - \frac{\pi}{2} + \frac{\pi}{2} \left.\right) = 4 cos \left(\right. \pi t \left.\right)\) (cm/s)
b. Phương trình dao động điều hòa có dạng: \(x = A cos \left(\right. \omega t + \varphi \left.\right)\)
\(\Rightarrow x = \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} \left.\right)\) (cm)
Phương trình của gia tốc có dạng: \(a = \omega^{2} A cos \left(\right. \omega t + \varphi + \pi \left.\right)\)
\(\Rightarrow a = \pi^{2} . \frac{4}{\pi} cos \left(\right. \pi t - \frac{\pi}{2} + \pi \left.\right) = 4 \pi cos \left(\right. \pi t + \frac{\pi}{2} \left.\right)\) (cm/s2)

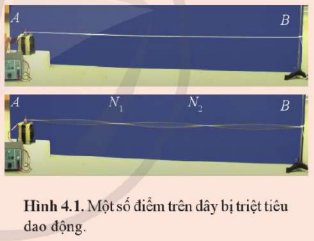




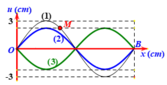
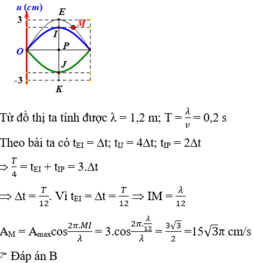

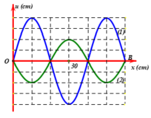


Hình 13.3 có 4 nút sóng và có 3 bụng sóng.