Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(\begin{array}{l}{c_1} = \frac{{16 + 21}}{2} = 18,5;{c_2} = \frac{{21 + 26}}{2} = 23,5;{c_3} = \frac{{26 + 31}}{2} = 28,5;\\{c_4} = \frac{{31 + 36}}{2} = 33,5;{c_3} = \frac{{36 + 41}}{2} = 38,5\end{array}\)
b) \({n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5} = 4.18,5 + 6.23,5 + 8.28,5 + 18.33,5 + 4.38,5 = 1200\).
c) \(\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}}}{{40}} = \frac{{1200}}{{40}} = 30\).

Cân nặng trung bình của học sinh sau khi ghép nhóm là:
\(\bar x = \frac{{4.47 + 5.51 + 7.55 + 7.59 + 5.63}}{{28}} = 55,6\left( {kg} \right)\)
Cân nặng trung bình của học sinh của mẫu số liệu gốc là:
\(\bar x = 56\left( {kg} \right)\)
Vậy giá trị ước lượng cân nặng trung bình của học sinh sau khi ghép nhóm xấp xỉ bằng cân nặng trung bình của học sinh của mẫu số liệu gốc.

Tham khảo:
a)

b) Không thể tính chính xác, chúng ta chỉ có thể tinh số gần đúng thời gian tự học trung bình của các học sinh trong lớp
c) Giá trị đại diện của nhóm bằng trung bình giá trị đầu mút phải và trái của nhóm đó
Nhóm \( \ge 4.5\) là nhóm mở nên ta dựa theo nhóm gần đó nhất là nhóm [3;4.5) để lấy giá trị đại diện

Số trung binh của mẫu số liệu: : \(\bar x = \frac{{0.75 \times 8 + 2.25 \times 23 + 2.75 \times 6 + 5.25 \times 3}}{{40}} = 2.25\).

Tổng số học sinh: \(n = 8 + 10 + 16 + 24 + 13 + 7 + 4 = 82\)
• Điểm trung bình môn Toán của các học sinh lớp 11 trên là:
\(\bar x = \frac{{8.6,75 + 10.7,25 + 16.7,75 + 24.8,25 + 13.8,75 + 7.9,25 + 4.9,75}}{{82}} = 8,12\)
• Nhóm chứa mốt của mẫu số liệu trên là nhóm \(\left[ {8;8,5} \right)\).
Do đó: \({u_m} = 8;{n_{m - 1}} = 16;{n_m} = 24;{n_{m + 1}} = 13;{u_{m + 1}} - {u_m} = 8,5 - 8 = 0,5\)
Mốt của mẫu số liệu ghép nhóm là:
\({M_O} = {u_m} + \frac{{{n_m} - {n_{m - 1}}}}{{\left( {{n_m} - {n_{m - 1}}} \right) + \left( {{n_m} - {n_{m + 1}}} \right)}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{24 - 16}}{{\left( {24 - 16} \right) + \left( {24 - 13} \right)}}.0,5 \approx 8,21\)
• Gọi \({x_1};{x_2};...;{x_{82}}\) là điểm của các học sinh lớp 11 được xếp theo thứ tự không giảm.
Ta có:
\(\begin{array}{l}{x_1},...,{x_8} \in \begin{array}{*{20}{c}}{\left[ {6,5;7} \right)}\end{array};{x_9},...,{x_{18}} \in \begin{array}{*{20}{c}}{\left[ {7;7,5} \right)}\end{array};{x_{19}},...,{x_{34}} \in \begin{array}{*{20}{c}}{\left[ {7,5;8} \right)}\end{array};{x_{35}},...,{x_{58}} \in \begin{array}{*{20}{c}}{\left[ {8;8,5} \right)}\end{array};\\{x_{59}},...,{x_{71}} \in \begin{array}{*{20}{c}}{\left[ {8,5;9} \right)}\end{array};{x_{72}},...,{x_{78}} \in \begin{array}{*{20}{c}}{\left[ {9;9,5} \right)}\end{array};{x_{79}},...,{x_{82}} \in \begin{array}{*{20}{c}}{\left[ {9,5;10} \right)}\end{array}\end{array}\)
Tứ phân vị thứ hai của dãy số liệu là: \(\frac{1}{2}\left( {{x_{41}} + {x_{42}}} \right)\)
Ta có: \(n = 82;{n_m} = 24;C = 8 + 10 + 16 = 34;{u_m} = 8;{u_{m + 1}} = 8,5\)
Do \({x_{41}},{x_{42}} \in \begin{array}{*{20}{l}}{\left[ {8;8,5} \right)}\end{array}\) nên tứ phân vị thứ hai của dãy số liệu là:
\({Q_2} = {u_m} + \frac{{\frac{n}{2} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 8 + \frac{{\frac{{82}}{2} - 34}}{{24}}.\left( {8,5 - 8} \right) \approx 8,15\)
Tứ phân vị thứ nhất của dãy số liệu là: \({x_{21}}\).
Ta có: \(n = 82;{n_m} = 16;C = 8 + 10 = 18;{u_m} = 7,5;{u_{m + 1}} = 8\)
Do \({x_{21}} \in \begin{array}{*{20}{l}}{\left[ {7,5;8} \right)}\end{array}\) nên tứ phân vị thứ nhất của dãy số liệu là:
\({Q_1} = {u_m} + \frac{{\frac{n}{4} - C}}{{{n_m}}}.\left( {{u_{m + 1}} - {u_m}} \right) = 7,5 + \frac{{\frac{{82}}{4} - 18}}{{16}}.\left( {8 - 7,5} \right) \approx 7,58\)
Tứ phân vị thứ ba của dãy số liệu là: \({x_{62}}\).
Ta có: \(n = 82;{n_j} = 13;C = 8 + 10 + 16 + 24 = 58;{u_j} = 8,5;{u_{j + 1}} = 9\)
Do \({x_{62}} \in \begin{array}{*{20}{l}}{\left[ {8,5;9} \right)}\end{array}\) nên tứ phân vị thứ ba của dãy số liệu là:
\({Q_3} = {u_j} + \frac{{\frac{{3n}}{4} - C}}{{{n_j}}}.\left( {{u_{j + 1}} - {u_j}} \right) = 8,5 + \frac{{\frac{{3.82}}{4} - 58}}{{13}}.\left( {9 - 8,5} \right) \approx 8,63\)

Đáp án D
Phương pháp:
TH1: An và Cường trả lời đúng, Bình trả lời sai.
TH2: Bình và Cường trả lời đúng, An trả lời sai.
Áp dụng quy tắc cộng.
Cách giải:
TH1: An và Cường trả lời đúng, Bình trả lời sai => P1 = 0,9.(1 - 0,7).0,8 = 0,216
TH2: Bình và Cường trả lời đúng, An trả lời sai => P2 = (1 - 0,9).0,7.0,8 = 0,056
Vậy xác suất cô giáo chỉ kiểm tra bài cũ đúng 3 bạn trên là P = P1 + P2 = 0,272

Chọn D
Gọi A là biến cố “Học sinh nhận được 6 điểm”.
Xác suất đánh đúng 1 câu là 1 4 và đánh sai 1 câu là 3 4 .
Để nhận được 6 điểm học sinh đó cần đánh đúng 12 câu và sai 8 câu.
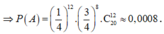

Có 2 bạn giỏi văn , 7 bạn giỏi toán, 3 bạn giỏi cả 2 môn
Có 2C1.7C1 =14 ( cách )



\(\bar x = \frac{{{n_1}{c_1} + {n_2}{c_2} + {n_3}{c_3} + {n_4}{c_4} + {n_5}{c_5}}}{{40}} = \frac{{1200}}{{40}} = 30\)
Vậy số câu trả lời đúng của các học sinh lớp 11A1 là 30 câu.