Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có: sin 2 α + c o s 2 α = 1
Suy ra: sin 2 α = 1 - c o s 2 α = 1 - 0 , 8 2 = 1 – 0,64 = 0,36
Vì sin α > 0 nên sin α = 0 , 36 = 0,6
Suy ra: tg α = sin α /cos α = 0,6/0,8 = 3/4 = 0,75
cotg α = 1/tg α = 1/0,75 = 1,3333
Đặt \(x=\alpha\)
a: \(\dfrac{1}{\cos^2x}=1+\tan^2x=1+\dfrac{1}{9}=\dfrac{10}{9}\)
nên \(\cos x=\dfrac{3\sqrt{10}}{10}\)
=>\(\sin x=\dfrac{\sqrt{10}}{10}\)
b: \(\dfrac{1}{\sin^2x}=1+\cot^2x=1+\dfrac{9}{16}=\dfrac{25}{16}\)
\(\Leftrightarrow\sin x=\dfrac{4}{5}\)
hay \(\cos x=\dfrac{3}{5}\)
Ta có: sin2α + cos2α = 1
Suy ra: sin2α = 1 – cos2α = 1 – (0,8)2 = 1 – 0,64 = 0,36
Vì sin α > 0 nên sin α = √0,36 = 0,6
Suy ra: tg α = sinα/cosα = 0,6/0,8 = 3/4 = 0,75
cotg α = 1/tgα = 1/0,75 = 1,3333
\(A=\left(\sin\alpha+\cos\alpha+\sin\alpha-\cos\alpha\right)^2-2\left(\sin\alpha+\cos\alpha\right)\left(\sin\alpha-\cos\alpha\right)\)
\(=4\sin^2\alpha-2\sin^2\alpha+2\cos^2\alpha=2\left(\sin^2\alpha+\cos^2\alpha\right)=2\)
\(B=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=\sin^4\alpha+\cos^4\alpha+2\sin^2\alpha.\cos^2\alpha\)
\(=\left(\sin^2\alpha+\cos^2\alpha\right)^2-1=0\)
\(C=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\left(\sin^2\alpha+\cos^2\alpha\right)=3\left(\sin^4\alpha+\cos^4\alpha\right)-2\sin^2\alpha.\cos^2\alpha\)
\(=3\left(\sin^2\alpha+\cos^2\alpha-\frac{1}{9}\right)^2-\frac{1}{9}=\frac{61}{27}\)
\(\sin\alpha=\frac{2}{3}\) nên a là góc nhọn trong tam giác vuông có cạnh đối là 2, cạnh huyền là 3 suy ra cạnh kề = \(\sqrt{5}\)
Vậy: \(\cos\alpha=\sqrt{\frac{5}{3}};\tan\alpha=\frac{2}{\sqrt{5}};\cot\alpha=\sqrt{\frac{5}{2}}\)
\(\frac{1-tana}{1+tana}=\frac{1-\frac{sina}{cosa}}{1+\frac{sina}{cosa}}=\frac{\frac{1}{cosa}\left(cosa-sina\right)}{\frac{1}{cosa}\left(cosa+sina\right)}=\frac{cosa-sina}{cosa+sina}\)
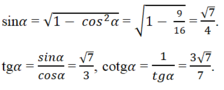
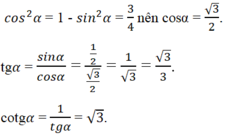
Vì tg α = 1/3 nên α là góc nhọn của một tam giác vuông có các cạnh góc vuông là 1 và 3.
Suy ra cạnh huyền của tam giác vuông là: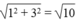
= 3,1623
Vậy: sin α = 3/5 ≈ 0,6 cos α = 4/5 ≈ 0,8