VB
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
20 tháng 4 2017
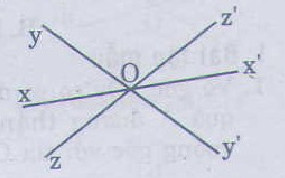
Trên hình vẽ, ba đường thẳng xx', yy', zz' cùng đi qua điểm O. Tên các cặp góc bằng nhau là:
ˆxOy=ˆx′Oy′,ˆyOz=ˆy′Oz′xOy^=x′Oy′^,yOz^=y′Oz′^;
ˆzOx′=ˆz′Ox,ˆxOz=ˆx′Oz′zOx′^=z′Ox^,xOz^=x′Oz′^;
ˆyOx′=ˆy′Ox,ˆzOy′=ˆz′OyyOx′^=y′Ox^,zOy′^=z′Oy^;
ˆxOx′=ˆyOy′=ˆzOz′(=180∘)xOx′^=yOy′^=zOz′^(=180∘).
16 tháng 1 2017
a) Vì d là đường trug trực của AB mà C,D thuộc d nên: AC=BC =>tam giác ACB cân tại C=> Góc CAB= góc CBA (1)
AD=BD=>tam giácABD cân tại D=> Góc DAB= góc DBA (2)
TỪ (1) và
AA
2 tháng 1 2018
bài 9:bạn tự vẽ hình nha!
xét tam giác ADC và tam giác ABE có:
AD=AB(gt)
\(\widehat{CAD}\)=\(\widehat{BAE}\) (bằng góc 90 độ + góc BAC)
AC=AE(gt)
=>tam giác ADC=ABE(cgc) =>BE=DC(hai cạnh tương ứng)và \(\widehat{ACD}\) = \(\widehat{AEB}\) (HAI GÓC TƯƠNG ỨNG)
Gọi giao điểm của DC và BE là I,AC và BE là H
Xét tam giác AHE và IHC có: góc HAE+AHE+AEH=góc CIH+CHI+HCI=180
mà AEH=ICH(CHỨNG MINH TRÊN),AHE=CHI(đối đỉnh) => EAI=HIC=90 độ => DC\(\perp\)BE
VẬY ĐƯỢC ĐIỀU PHẢI CHỨNG MINH
21 tháng 8 2017
Bài này đúng ko
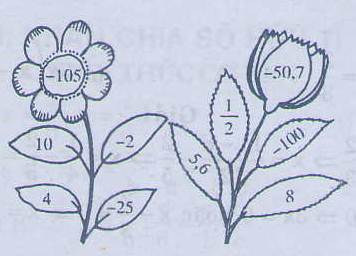
Em hãy tìm cách " nối" các số ở những chiếc là bằng dấu các phép tính cộng, trừ, nhân, chia và dấu ngoặc để được một biểu thức có giá trị đúng bằng số ở bông hoa?
Giải
Có nhiều cách nối, chẳng hạn:
4.(-25) + 10 : (-2)
= -100 + (-5)
= -105
\(\frac{1}{2}\) (-100) - 5,6 : 8
= -50 - 0,7
= -50 + (-0,7)
= -50,7
17 tháng 5 2017
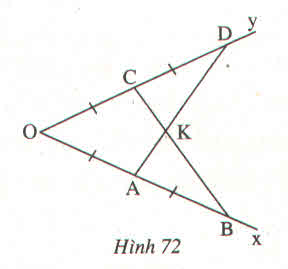
Vì OA = AB = OC = CD
=> OD = OB
Xét \(\Delta OAD\)và \(\Delta OCB\)có:
OA = OC (gt)
\(\widehat{O}\)(chung)
OD = OB (cmt)
Do đó: \(\Delta OAD=\Delta OCB\) (c-g-c)
=> \(\widehat{ODA}=\widehat{OBC}\) (2 cạnh tương ứng)
=> \(\widehat{OCB}=\widehat{OAD}\) (2 cạnh tương ứng)
Vì \(\widehat{OCB}=\widehat{OAD}\) mà \(\widehat{OCB}+\widehat{DCB}=180^0\)(kề bù)
và \(\widehat{OAD}+\widehat{DAB}=180^0\)(kề bù)
Do đó: \(\widehat{DAB}=\widehat{BCD}\)
Xét \(\Delta KAB\)và \(\Delta KCD\)có:
\(\widehat{ODA}=\widehat{OBC}\)(cmt)
AB = CD (gt)
\(\widehat{CDK}=\widehat{ABK}\left(\widehat{ODA}=\widehat{OBC}\right)\)
Do đó: \(\Delta KAB=\Delta KCD\left(g-c-g\right)\)
=> CK = KA (2 cạnh tương ứng)
Xét \(\Delta OCK\)và\(\Delta OAK\)có:
CK = KA(cmt)
OK (chung)
OA = OC (gt)
Do đó: \(\Delta OCK=\Delta OAK\left(c-c-c\right)\)
=> \(\widehat{COK}=\widehat{AOK}\) ( 2 góc tương ứng )
=> OK là tia phân giác \(\widehat{O}\)