Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

*Cho số phức z = a + bi.
Ta gọi số phức a – bi là số phức liên hợp của z và kí hiệu là .
Vậy ta có z = a + bi thì ¯zz¯ = a – bi
*Số phức z bằng số phức liên hợp của nó ⇔ a = a và b = -b
⇔ a ∈ R và b = 0 ⇔ z là một số thực.

- Tính chất của hàm số mũ y= ax ( a > 0, a# 1).
- Tập xác định: .
- Đạo hàm: ∀x ∈ ,y’= axlna.
- Chiều biến thiên Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
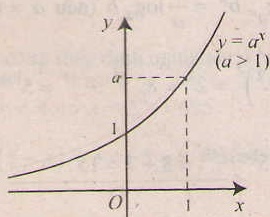
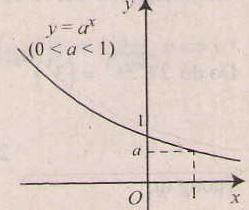
- Tiệm cận: trục Ox là tiệm cận ngang.
- Đồ thị nằm hoàn toàn về phía trên trục hoành ( y= ax > 0, ∀x), và luôn cắt trục tung taih điểm ( 0;1) và đi qua điểm (1;a).
- Tính chất của hàm số lôgarit y = logax (a> 0, a# 1).
- Tập xác định: (0; +∞).
- Đạo hàm ∀x ∈ (0; +∞),y’ = .
- Chiều biến thiên: Nếu a> 1 thì hàm số luôn đồng biến
Nếu 0< a < 1 thì hàm số luôn nghịch biến
- Tiệm cận: Trục Oy là tiệm cận đứng.
- Đồ thị nằm hoàn toàn phía bên phải trục tung, luôn cắt trục hoành tại điểm (1;0) và đi qua điểm (a;1).
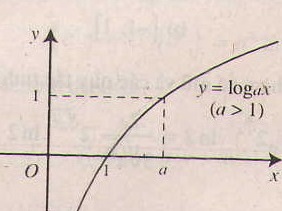
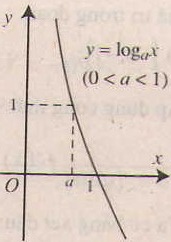

Hàm số mũ: y = a x
- Tập xác định: D = R.
- Chiều biến thiên:
+ y = a x .lna
a > 1 ⇒ y’ > 0 ⇒ Hàm số đồng biến trên R.
0 < a < 1 ⇒ y’ < 0 ⇒ Hàm số nghịch biến trên R.
+ Tiệm cận: 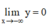
⇒ y = 0 (trục Ox) là tiệm cận ngang của đồ thị hàm số.
- Đồ thị:
+ Đồ thị đi qua (0; 1) và (1; a).
+ Đồ thị nằm phía trên trục hoành.

Lời giải:
Cho hàm số y= f(x) liên tục trên [a; b] , F(x) là một nguyên hàm của f(x) trên [a; b]. Hiệu số F(b) – F(a) được gọi là tích phân từ a đến b của hàm số f(x), kí hiệu là ∫abf(x)dx.
Ta có: ∫abf(x)dx=F(x)ab=F(b)-F(a)
Ta gọi ∫ab là dấu tích phân, a là cận dưới, b là cận trên, f(x)dx biểu thức dưới dấu tích phân, f(x) là hàm số dưới dấu tích phân.
2.Các tính chất
1. ∫aaf(x)dx=0
2. ∫abf(x)dx=- ∫baf(x)dx
3. ∫bakf(x)dx=k. ∫baf(x)dx ( k là hằng số)
4. ∫ab[f(x)±g(x)]dx= ∫abf(x)dx± ∫abg(x)dx
5. ∫abf(x)dx= ∫acf(x)dx+ ∫abf(x)dx(a<c<b)
Các tính chất của phép cộng