
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Do dãy 2000 số tự nhiên liên tiếp đó không có số nguyên tố nào nên chúng là hợp số.
Coi dãy đó chứa các số tự nhiên liên tiếp từ a + 2 đến a + 2001 \(\left(a\in N\right)\)
Để tất cả các số trên là hợp số thì a phải chia hết các số từ 2 đến 2001, vì vậy a = 2001!
Thế vào các số trên, ta có:
- a + 2 = 2001! + 2 = 2 ( 3 * 4 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
- a + 3 = 2001! + 3 = 3 ( 2 * 4 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
- a + 4 = 2001! + 4 = 4 ( 2 * 3 * 5 * ... * 2001 + 1 ) ( là hợp số ) - thoả mãn
...................................................................................................................................
- a + 2001 = 2001! + 2001 = 2001 ( 2 * 3 * 4 * ... * 2000 + 1 ) ( là hợp số ) - thoả mãn
Vậy trong tập hợp số tự nhiên, dãy có 2000 số tự nhiên liên tiếp mà không có 1 số nguyên tố nào là:
2001! + 2 ; 2001! + 3 ; 2001! + 4 ; .... ; 2001! + 1999 ; 2001! + 2000 ; 2001! + 2001

mình chỉ bạn nè. Bạn vào trang này nè: http://www.van.edu.vn/cam-nhan-cua-em-ve-tuy-but-mua-xuan-cua-toi-cua-vu-bang.html.
Mình không biết đúng yêu cầu của bạn không nhưng có thể nó sẽ giúp được bạn
CHÚC BẠN HỌC TỐT NHÉ
nhớ k mình nha

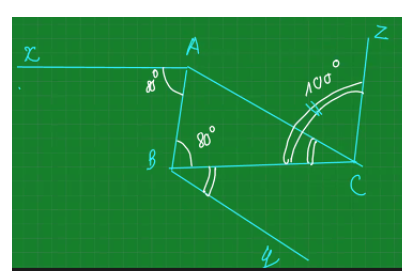
Ta có: \(\widehat{BAx}=\widehat{ABC}=80^0\)
Mà 2 góc này là 2 góc so le trong
=> Ax//BC
Ta có: \(\widehat{ABC}+\widehat{BCz}=80^0+100^0=180^0\)
Mà 2 góc này là 2 góc trong cùng phía
=> AB//Cz

bài làm thế này có được không
Về trường Trung học cơ sở Nguyễn Bỉnh Khiêm, thuộc phường Hoà Minh - Quận Liên Chiểu, tôi được nghe những câu chuyện cảm động của các em học sinh (HS) nghèo, hoàn cảnh gia đình rất khó khăn nhưng vẫn vươn lên học giỏi toàn diện.
Trong đó một em đã để lại ấn tượng cho tôi nhiều nhất là em Lê Hồng Ân, học lớp 6/3. Mặc dù gia đình em có hoàn cảnh rất khó khăn, một mình mẹ em phải bươn chải kiếm tiền nuôi hai chị em ăn học. Như cô Phan Thị Lệ, mẹ em tâm sự: “Nhà cửa và mọi thứ đồ đạc trong nhà đều do người thân mua cho.Tôi làm công nhân ở khu công nghiệp tiền lương rất ít, phải chi tiêu thật tiết kiệm mới có tiền để hai con ăn học. Nhiều khi em Ân phải nhịn ăn sáng để dành tiền mua dụng cụ học tập. Nhưng tôi hạnh phúc là có được một đứa con học giỏi và ngoan hiền đến như vậy.”
Hoàn cảnh gia đình khó khăn là vậy nhưng em Ân trong sáu năm liền là học sinh giỏi toàn diện của trường. Và hằng năm em luôn được thành phố trao học bổng học sinh hiếu học, có tinh thần vượt khó trong học tập. Ngoài ra, em còn được nhận học bổng từ các Hội khuyến học Quận, công ty bia Huế, công ty nhà máy nhựa,…
Em không chỉ là một học sinh ngoan hiền, học giỏi mà còn là một HS tham gia rất năng nổ các hoạt động của trường giao phó. Như cô Tổng phụ trách Hệ Thị Mỹ Đức nhận xét: “Em là một liên đội trưởng xuất sắc nhất của trường Tiểu học Duy Tân. Đến lớp 6 em vừa là một lớp trưởng, vừa là một chi đội trưởng rất năng động, nhiệt tình. Và em là một học sinh có nhiều đóng góp trong những phong trào của đoàn trường”.
Ân học giỏi toàn diện các môn, trong đó đáng biểu dương là em thi được giải ba học sinh giỏi cấp thành phố năm lớp 5. Ngoài ra, em còn có tố chất năng khiếu rất nhiều lĩnh vực như vẽ, đàn, sáng tạo dụng cụ học tập, các phong trao thể thao,… . Đặc biệt là phong trào thể thao em đã được giải nhì bóng bàn năm lớp 4, đến lớp 6 em được giải ba cấp quận.
Em đứng đầu trong việc làm báo tường của lớp với những hình vẽ rất đẹp và có ý nghĩa.
Là một HS giỏi và có phẩm chất đạo đức tốt nên em rất được các thầy cô giáo và bạn bè trong trường quý mến. Cô Phan Thị Mỹ Vân, chủ nhiệm lớp nhận xét: “Em là một học sinh rất ngoan hiền, học giỏi tất cả các môn. Và là học sinh có kết quả học tập trong học kì I năm học 2008- 2009 cao nhất trường (9,5). Ngoài ra, em còn là một lớp trưởng rất năng động, nhiệt tình vì vậy mà tôi rất yên tâm khi giao cho em công việc điều hành lớp”. Mặt khác, em là một học sinh rất giàu lòng tương thân tương ái, sẵn sàng giúp đỡ những bạn học sinh yếu kém trong lớp vươn lên trong học tập. Như em Nguyễn Quang Đạt, bạn cùng lớp em đã khen ngợi: “Ân là một người bạn rất tốt, nhiệt tình giúp đỡ em trong học tập. Và từ việc học nhóm với Ân mà em đã tiến bộ hơn rất nhiều”.
Ân là một học sinh không chỉ giỏi mà còn rất ham học và có tinh thần vượt khó. Ở trường, em là một học sinh giỏi, ngoan hiền được thầy cô bạn bè quý mến. Còn ở nhà em là một đứa con hết mực hiếu thảo, em luôn làm những công việc nhà khi mẹ đi vắng. Dù là còn nhỏ tuổi nhưng em nhận thức được hoàn cảnh khó khăn, thiếu thốn của gia đình vì thế mà em đã ra sức nổ lực học tập. Và em đã bộc lộ ước mơ của mình: “Em sẽ cố gắng học thật giỏi để trở thành một kiến trúc sư, đáp ứng được lòng mong mỏi của gia đình, thầy cô và bạn bè. Và để mẹ em đỡ khổ và vất vả hơn.”
Với khả năng học giỏi toàn diện và nổ lực “vượt lên trên hoàn cảnh” cùng với sự dạy bảo của các thầy cô giáo, sự giúp đỡ của các cơ quan ban ngành, đoàn thể … Tôi tin rằng Ân sẽ thực hiện được ước mơ của mình. Tinh thần hiếu học và nghị lực vươn lên không ngừng của Ân thật đáng khâm phục. Đó là tấm gương sáng để cho các bạn học sinh noi theo...

Bạn tự vẽ hình nhé.
K là giao điểm của 2 đường phân giác BD và CE => AK là phân giác của góc A (Vì 3 đường phân giác đồng quy tại 1 điểm)
Mà tam giác ABC cân tại A => Phân giác góc A cũng chính là trung tuyến => AK qua trung điểm của BC
(Hoặc bạn có thể chứng minh cụ thể như sau: Kéo dài AK cắt BC tại M
Xét 2 t.g AMB và AMC có:
- AM chung
- g. BAM = CAM (vì AK là phân giác; K thuộc AM)
-AB = AC (2 cạnh bên của tam giác cân ABC)
=> t.g AMB = t. AMC (C.G.C) => MB = MC => M là trung điểm của BC.)
 Mong mọi người giúp đỡ mình ! Mình cảm ơn !
Mong mọi người giúp đỡ mình ! Mình cảm ơn !
Ta có \(\frac{a}{b}=\frac{c}{a}=\frac{d}{c}\Rightarrow\left(\frac{a}{b}\right)^2=\left(\frac{c}{a}\right)^2=\left(\frac{d}{c}\right)^2\Rightarrow\frac{a^2}{b^2}=\frac{c^2}{a^2}=\frac{d^2}{c^2}=\frac{a^2+c^2+d^2}{b^2+a^2+c^2}\)
=> \(\frac{a^2}{b^2}=\frac{a^2+c^2+d^2}{a^2+b^2+c^2}\)
<=> \(\frac{a}{b}.\frac{c}{a}=\frac{c}{b}=\frac{a^2+b^2+d^2}{b^2+a^2+c^2}\)