Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

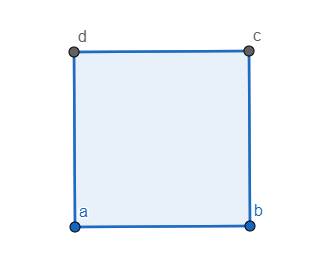
Xét 1 mặt bất kì của khối lập phương như hình vẽ và gọi 4 số ở đỉnh là a, b, c, d. Khi đó do \(a+b+c,b+c+d,c+d+a,d+a+b\ge10\) nên \(3\left(a+b+c+d\right)\ge40\) \(\Rightarrow a+b+c+d\ge14\)
Làm tương tự cho 4 mặt còn lại, ta đều được tổng của 4 số trên mỗi mặt đều không nhỏ hơn 14.
Nhưng trong một mặt, sẽ có mặt có chứa đỉnh mang số 8. Khi đó 3 đỉnh còn lại bắt buộc là 1, 2, 3, mà \(1+2+3< 10\), vô lí. Lập luận tương tự cho trường hợp GTNN là 15, 16, 17. Nếu GTNN là 18, ta chỉ ra 1 trường hợp dấu "=" xảy ra:
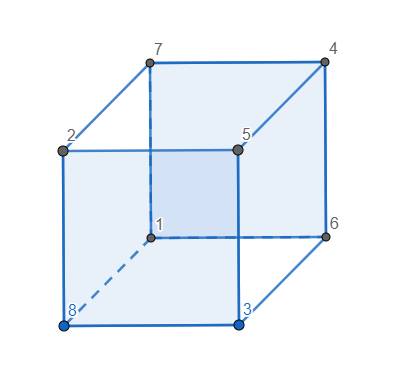
Vậy GTNN của 4 số trong cùng 1 mặt là 18.

a) Vẽ đồ thị
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA = . (-1,5)2 =
. 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, = . 1,52 =
. 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.

a) Vẽ đồ thị
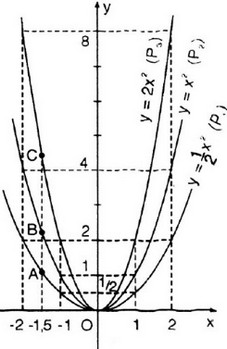
b) Gọi yA, yB, yC lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:
yA =  . (-1,5)2 =
. (-1,5)2 =  . 2,25 = 1,125
. 2,25 = 1,125
yB = (-1,5)2 = 2,25
yC = 2 (-1,5)2 = 2 . 2,25 = 4,5
c) Gọi yA, yB, yC’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:
yA, =  . 1,52 =
. 1,52 =  . 2,25 = 1,125
. 2,25 = 1,125
yB, = 1,52 = 2,25
yC’ = 2 . 1,52 = 2 . 2,25 = 4,5
Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.
d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.
Vậy x = 0 thì hàm số có giả trị nhỏ nhất.

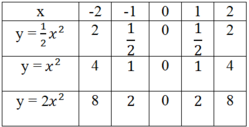
a) Bảng giá trị tương ứng của x và y:
Vẽ đồ thị:
Trên mặt phẳng lưới lấy các điểm (-2; 2); (-1; ½); (0; 0); (1; 1/2); (2; 2), nối chúng thành một đường cong ta được đồ thị hàm số y = ½.x2.
Lấy các điểm (-2; 4); (-1; 1); (0; 0); (1; 1); (2; 4), nối chúng thành một đường cong ta được đồ thị hàm số y = x2.
Lấy các điểm (-2; 8); (-1; 2); (0; 0); (1; 2); (2; 8), nối chúng thành một đường cong ta được đồ thị hàm số y = 2x2.
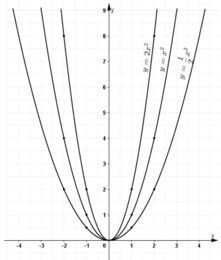
b) Lấy các điểm A, B, C lần lượt nằm trên 3 đồ thị và có hoành độ bằng -1,5.
Từ điểm (-1,5;0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị 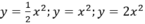 lần lượt tại các điểm A,B,C.
lần lượt tại các điểm A,B,C.
Gọi yA,yB,yC lần lượt là tung độ của các điểm A,B,C. Ta có:
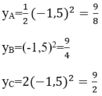
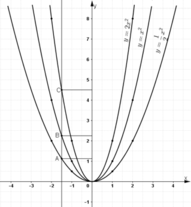
Khi đó tung độ điểm A bằng 9/8; tung độ điểm B bằng 9/4; tung độ điểm C bằng 9/2
c)
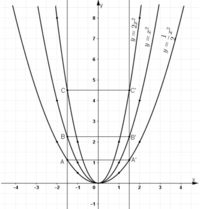
Lấy các điểm A’, B’, C’ lần lượt nằm trên 3 đồ thị và có hoành độ bằng 1,5.
Từ điểm (1,5;0) nằm trên trục hoành ta kẻ đường thẳng song song với Oy. Đường thẳng này cắt các đồ thị 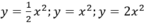 lần lượt tại các điểm A,B,C.
lần lượt tại các điểm A,B,C.
Gọi yA,yB,yC lần lượt là tung độ của các điểm A,B,C. Ta có:
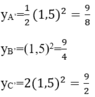
Khi đó 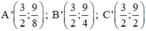
Nhận xét: A và A’; B và B’; C và C’ đối xứng nhau qua trục Oy.
d) Hàm số có giá trị nhỏ nhất ⇔ y nhỏ nhất.
Dựa vào đồ thị nhận thấy cả ba hàm số đạt y nhỏ nhất tại điểm O(0; 0).
Vậy ba hàm số trên đều đạt giá trị nhỏ nhất tại x = 0.

Trên mặt phẳng cho n > = điểm sao cho khoảng cách giữa 2 điểm bất kì đôi một khác nhau. Người ta nối mỗi điểm với điểm gần nhất.
CMR qua mỗi điểm co không quá 5 đoạn thẳng
ai cần acc roblox ko
có