Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét đoạn mạch gồm ba điện trở \(R_1,R_2,R_3\) mắc song song :
Ta có : \(I=I_1+I_2+I_3\)
\(U=U_1=U_2=U_3\) hay \(IR_{tđ}=I_1R_1=I_2R_2=I_3R_3\)
Vì \(I_1< I\), do đó \(R_{tđ}< R_1\).
Do \(I_2< I\) nên \(R_{tđ}< R_2\), tương tự với \(I_3< I\Rightarrow R_{tđ}< R_3\). (đpcm)
Cách khác cách của Minh :v
Trong đoạn mạch song song mắc n điện trở:
\(\dfrac{1}{R_{rđ}}=\dfrac{1}{R_1}+\dfrac{1}{R_2}+\dfrac{1}{R_3}+...+\dfrac{1}{R_n}\)
Ta có: \(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_1}\Rightarrow R_{tđ}< R_1\)
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_2}\Rightarrow R_{tđ}< R_2\)
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_3}\Rightarrow R_{tđ}< R_3\)
...
\(\dfrac{1}{R_{tđ}}>\dfrac{1}{R_n}\Rightarrow R_{tđ}< R_n\)
Do đó điện trở tương đương của đoạn mạch song song nhỏ hơn điện trở mỗi thành phần.

Pạn dựa vào địh nghĩa điện trở tươg đươg trog đoạn mạch song2 mà giải bt này nké

Đối với đoạn mạch gồm hai điện trở mắc song song, hiệu điện thế giữa hai đầu điện trở R1 bằng hiệu điện thế giữa hai đầu R2, tức là U1 = U2. Từ đó ta có I1R1 = I2R2, suy ra \(\dfrac{I_1}{I_2}=\dfrac{R_1}{R_2}\)

* Trả lời:
Trong mạch nối tiếp ta có:
\(U=U_1+U_2=IR_1+IR_2=I\left(R_1+R_2\right)\)
Mặt khác \(U=IR_{tđ}\)
\(\Rightarrow R_{tđ}=R_1+R_2\)
Vì là đoạn mạch nối tiếp nên:
U = U1 + U2 = IR1 + IR2 = I(R1 + R2)
Ta có:
U = ỈR => Rtd = U/I = I(R1 + R2) / I = R1 + R2
Vay Rtd = R1 + R2

\(\Rightarrow\dfrac{1}{Rtd}=\dfrac{1}{R1}+\dfrac{1}{R2}+....+\dfrac{1}{R2021}\)
\(\Rightarrow\dfrac{1}{Rtd}=\dfrac{1}{1}+\dfrac{1}{\dfrac{1}{2}}+\dfrac{1}{\dfrac{1}{3}}+....+\dfrac{1}{\dfrac{1}{2021}}\)
\(\Rightarrow\dfrac{1}{Rtd}=1+2+3+....+2021\)
\(A=1+2+3+....+2021\)
\(A=2021+2020+2019+...+1\)
\(\Rightarrow2A=2022+2022+...+2022\)(co 2021 so 2022)
\(\Rightarrow2A=2022.2021\Rightarrow A=\dfrac{2022.2021}{2}=2043231\)
\(\Rightarrow\dfrac{1}{Rtd}=A\Rightarrow Rtd=4,89.10^{-7}\left(\Omega\right)\)

có \(R1//R2=>\left\{{}\begin{matrix}I=I1+I2\\U=U1=U2\end{matrix}\right.\)
\(=>I=I1+I2\)
\(=>\dfrac{U}{Rtd}=\dfrac{U1}{R1}+\dfrac{U2}{R2}\)
\(=>\dfrac{U}{Rtd}:U=\dfrac{U}{R1}:U+\dfrac{U}{R2}:U\)
\(=>\dfrac{1}{Rtd}=\dfrac{1}{R1} +\dfrac{1}{R2}=>\dfrac{1}{Rtd}=\dfrac{R1+R2}{R1.R2}\)
\(=>Rtd=\dfrac{R1.R2}{R1+R2}\)

Theo định luật Ôm : \(I=\dfrac{U}{R}\Rightarrow U=I.R\)
nên \(U_1=I_1R_1\)
\(U_2=I_2R_2\)
\(\Rightarrow\) \(\dfrac{U_1}{U_2}=\dfrac{I_1R_1}{I_1R_2}\)
mà \(R_1\) nt \(R_2\) nên \(I_1=I_2\) :
\(\Rightarrow\) \(\dfrac{U_1}{U_2}=\dfrac{R_1}{R_2}\left(đpcm\right)\)
Trong mạch mắc nối tiếp, cường độ dòng điện chạy qua R1 và R2 là như nhau, ta có
I = , từ đó suy ra


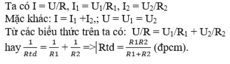
Trong mạch gồm hai điện trở R2, R3 mắc song song, cường độ dòng điện chạy qua các điện trở là: \(I_1=\dfrac{U_1}{R_1}\) và \(I_2=\dfrac{U_2}{R_2}\), trong đó U1 = U2.
Cường độ dòng điện chạy qua đoạn mạch là I = I1 + I2 = \(\dfrac{U}{R_1}+\dfrac{U}{R_2}\) = \(\dfrac{U}{R_{td}}\). Từ đó ta có \(\dfrac{1}{R_{td}}\) = \(\dfrac{1}{R_1}+\dfrac{1}{R_2}\)
Suy ra: \(R_{td}=\dfrac{R_1R_2}{R_1+R_2}\)
Dựa vào t/c mạch // U=U1=U2=U3