
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có :
37! = 1.2.3.4....36.37 = (2.5).(15.8).(24.4).(35.6).(10.20.30).3.7.9....( các số còn lại)
= 10.120.100.210.(...000).(các số còn lại) = ...00000000
Vậy 8 chữ số cuối cùng của 37! là 8 số 0

Mỗi đơn vị được chia thành 10 phần bằng nhau nên khoảng cách giữa 2 vạch chia liên tiếp là 0,1 đơn vị.
a) Điểm A biểu diễn số 13,4
Điểm B biểu diễn số 14,2
b) Làm tròn số thập phân được biểu diễn bởi điểm C với độ chính xác 0,05, ta được 14,6 (vì điểm C nằm gần vạch biểu thị số 14,6 nhất).

a)\(\frac{{15}}{8} = 1,875;\,\,\,\,\,\,\,\frac{{ - 99}}{{20}} = - 4,95;\,\,\,\,\,\,\\\frac{{40}}{9} = 4,\left( 4 \right);\,\,\, - \frac{{44}}{7} = - 6,(285714)\)
b) Trong các số thập phân trên, số thập phân 4,(4) và -6,(285714) là các số thập phân vô hạn tuần hoàn với chu kì lần lượt là 4 và 285714

a) Các số hữu tỉ được biểu diễn bằng các số thập phân hữu hạn hoặc vô hạn tuần hoàn.
b) Các số vô tỉ được biểu diễn bằng các số thập phân vô hạn không tuần hoàn.
a) Số hữu tỉ được biểu diễn dưới dạng số thập phân hữu hạn hoặc vô hạn tuần hoàn
b) Số vô tỉ được biểu diễn dưới dạng số thập phân vô hạn không tuần hoàn

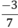 là :
là :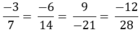
là 8 chữ số 0