
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Tọa độ vecto pháp tuyến của \(\Delta \) là:
Tọa độ vecto chỉ phương của \(\Delta \) là:
b) Chọn \(x = 0;x = 1\) ta lần được được 2 điểm A và B thuộc đường thẳng \(\Delta \) là: \(A\left( {0;1} \right),B\left( {1;2} \right)\)

a) Do MH vuông góc với đường thẳng \(\Delta \) nên ta có vecto chỉ phương của MH là: \(\overrightarrow u = \left( {2;1} \right)\)
b) Phương trình tham số của đường thẳng MH đi qua \(M\left( { - 1;1} \right)\) có vecto chỉ phương\(\overrightarrow u = \left( {2;1} \right)\) là: \(\left\{ \begin{array}{l}x = - 1 + 2t\\y = 1 + t\end{array} \right. \Leftrightarrow x - 2y + 3 = 0\)
c) H là giao điểm của MH và đường thẳng \(\Delta \)
Xét hệ phương trình: \(\left\{ \begin{array}{l}x - 2y + 3 = 0\\2x + y - 4 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\) . Vậy tọa độ điểm H là: \(H\left( {1;2} \right)\)
Độ dài đoạn thẳng MH là: \(MH = \sqrt {{{\left( {1 + 1} \right)}^2} + {{\left( {2 - 1} \right)}^2}} = \sqrt {{2^2} + {1^2}} = \sqrt 5 \)

Ta có \(\Delta :y = 3x + 4 \Leftrightarrow \Delta :3x - y + 4 = 0\)
Vậy vectơ pháp tuyến của \(\Delta \) là \(\overrightarrow n = \left( {3; - 1} \right)\).

Đường thẳng đã cho có VTPT là n → ( 2; 6) nên có VTCP là u → ( 6; -2)
Mà vecto u 1 → ( 3; -1) cùng phương với vecto u → nên vecto này cũng là VTCP của đường thẳng đã cho..
Chọn D.

a) Xét hệ phương trình: \(\left\{ \begin{array}{l}y = 0\\y = ax + b\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 0\\x = \frac{{ - b}}{a}\end{array} \right.\) . Vậy đường thẳng \(\Delta \) cắt trục hoành tại điểm \(\left( {\frac{{ - b}}{a};0} \right)\).
b) Phương trình đường thẳng \({\Delta _o}\) đi qua O(0, 0) và song song (hoặc trùng) với\(\Delta \) là \(y = a\left( {x - 0} \right) + 0 = {\rm{a}}x\).
c) Ta có: \({\alpha _\Delta } = {\alpha _{{\Delta _o}}}\).
d) Từ câu b) và điều kiện \(x_o^2 + y_o^2 = 1\) trong đó \({y_o}\) là tung độ của điểm M, ta suy ra \({x_o} \ne 0\). Do đó: \(\tan {\alpha _\Delta } = \tan {\alpha _{{\Delta _o}}} = \frac{{{y_o}}}{{{x_o}}} = a\).

a) Vector chỉ phương \(\overrightarrow{u}\left(4;-2\right)\)
=> Vector pháp tuyến \(\overrightarrow{n}\left(2;4\right)\)
Phương trình (d) : 2(x + 1) + 4(y - 1) = 0
<=> x + 2y - 1 = 0
b) \(d\left(M,\Delta\right)=\dfrac{\left|3.\left(-1\right)-4.1-3\right|}{\sqrt{3^2+\left(-4\right)^2}}=2\)
c) Do đường thẳng \(d_1\perp\Delta\)
nên \(\overrightarrow{u}\left(4;-2\right)\) là vector pháp tuyến của (d1)
Phương trình tổng quát :
4(x + 1) - 2(y - 2) = 0
<=> 2x - y + 4 = 0

a) Giao điểm d1 và d2
\(\left\{{}\begin{matrix}x+3y-1=0\\x-3y-5=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\) => A (-2;1)
Đường thẳng d3 có \(\overrightarrow{n_{d3}}=\left(2;-1\right)\) . Delta vuông góc với d3 nên có
\(\overrightarrow{u_{\Delta}}=\left(2;-1\right)\) \(\Rightarrow\overrightarrow{n_{\Delta}}=\left(-1;-2\right)\)
PTđt delta
\(-1\left(x+2\right)+\left(-2\right)\left(y-1\right)=0\)
\(\Leftrightarrow-x-2y+1=0\)
b) Tương tự, tìm được đường thẳng delta đi qua B(-1;-1)
Hệ số k = tan45 = 1 .
Tự xử nốt
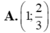


Ta có: \(\overrightarrow {{n_\Delta }} = \left( {2; - 1} \right)\), suy ra \(\overrightarrow {{u_\Delta }} = \left( {1;2} \right)\).