
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cặp tam giác vuông ở hình d. Vì cạnh huyền và một cạnh góc vuông của tam giác này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia

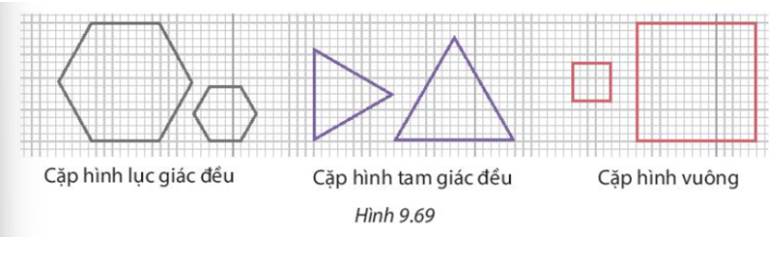
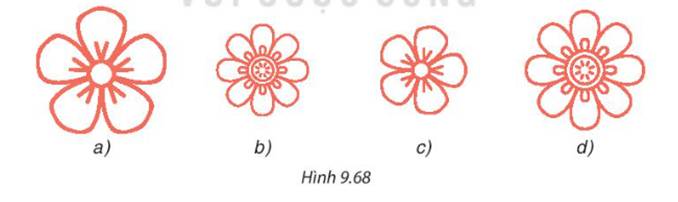
Cặp hình lục giác đều và cặp hình vuông là đồng dạng phối cảnh

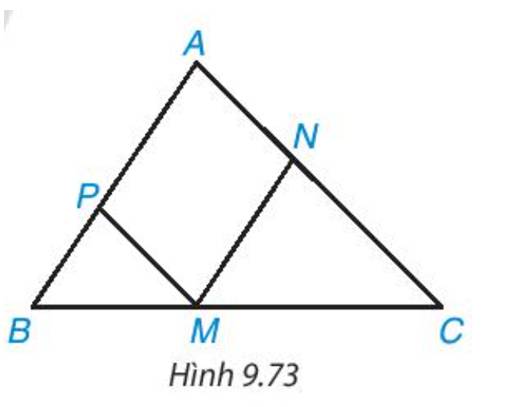
- ΔCNM ~ ΔCAB (vì MN // AB) (1)
- ΔMPB ~ ΔCAB (vì MP // AC) (2)
- Từ (1) và (2) => ΔCNM ~ ΔMPB

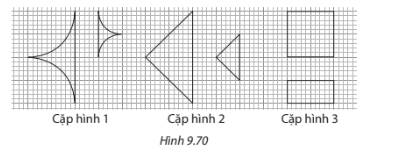
Cặp hình 1, 2 là cặp hình đồng dạng.
Cặp hình 2 là hình đồng dạng phối cảnh.

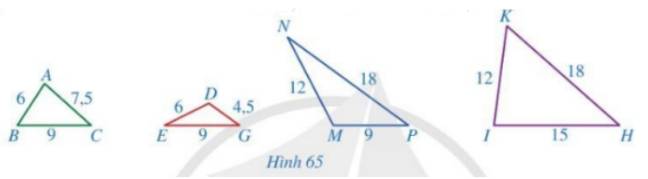
Xét tam giác ABC và tam giác IKH có:
\(\frac{{AB}}{{IK}} = \frac{{AC}}{{IH}} = \frac{{BC}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta ABC \backsim\Delta IKH\) (c-c-c)
Xét tam giác DEG và tam giác MNP có:
\(\frac{{DE}}{{MN}} = \frac{{DG}}{{MP}} = \frac{{EG}}{{KH}} = \frac{1}{2}\)
\( \Rightarrow \Delta DEG \backsim\Delta MNP\) (c-c-c)

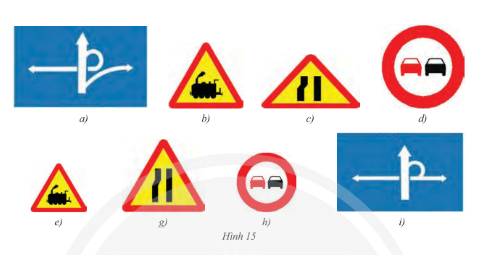
Các cặp hình đồng dạng là:
- Hình a và hình i đồng dạng với nhau;
- Hình b và hình e đồng dạng với nhau;
- Hình c và hình g đồng dạng với nhau;
- Hình d và hình h đồng dạng với nhau.

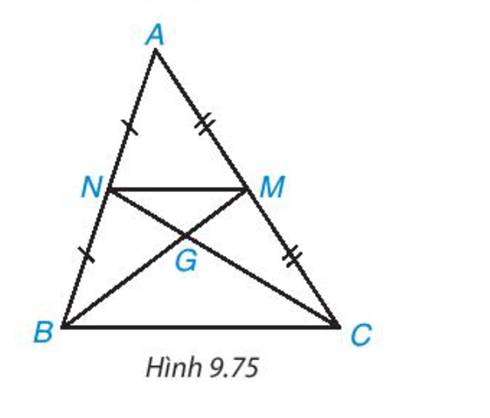
- Xét tam giác ABC có, NA=NB, MA=MC
=> NM là đường trung bình của tam giác ABC
=> NM // BC, \(NM = \frac{1}{2}AB\)
- Xét tam giác GMN và tam giác GBC có NM // BC => ΔGMN ∽ ΔGBC

Xét tam giác MPN có: \(\widehat P = {180^o} - \widehat M - \widehat N = {180^o} - {60^o} - {70^o} = {50^o}\)
Các cặp tam giác đồng dạng trong hình 9.22 là: \(\Delta ACB \backsim \Delta DF{\rm{E; }}\Delta {\rm{ACB}} \backsim \Delta {\rm{MP}}N;\Delta DF{\rm{E}} \backsim \Delta MPN\)
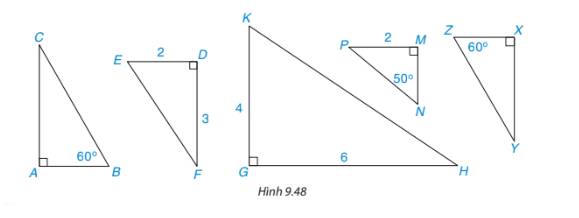
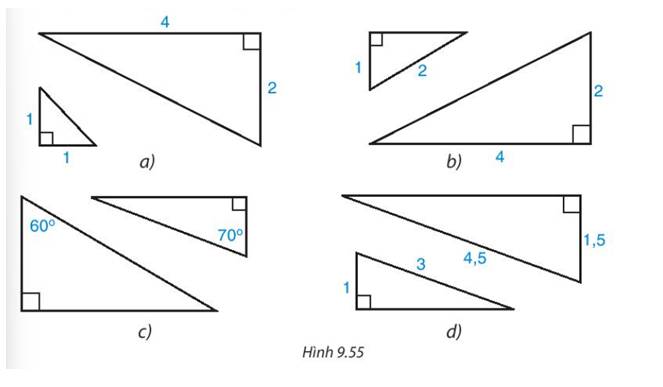

Các cặp tam giác vuông đồng dạng:
\(\begin{array}{l}\Delta ABC \backsim \Delta X{\rm{Z}}Y(\widehat A = \widehat X;\widehat B = \widehat Z)\\\Delta E{\rm{D}}F \backsim \Delta KGH\left( {\frac{{E{\rm{D}}}}{{KG}} = \frac{{DF}}{{GF}};\widehat {E{\rm{D}}F} = \widehat {KGH}} \right)\end{array}\)