Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xin lỗi mình viết nhầm đề:
Sô 184 được viết thành tổng của 3 số sao cho số hạng thứ nhất và số hạng thứ hai tỉ lệ thuận với 3 và 2. Số hạng thứ hai và số hạng thứ ba tỉ lệ thuận với 5 và 7. Tìm 3 số hạng

Số hạng thứ 1 là 1.
Số hạng thứ 2 cũng là 1.
Số hạng thứ 3 cũng là 1.
Số hạng thứ 4 là 3, bằng tổng của 3 số hạng trước đó (1 + 1 + 1).
Số hạng thứ 5 = 1 + 1 + 3 = 5
Số hạng thứ 6 = 1 + 3 + 5 = 9
Số hạng thứ 7 = 3 + 5 + 9 = 17 .Và cứ tiếp tục như vậy.
Ta luôn nhận được dãy số sau: 1, 1, 1, 3, 5, 1, 1, 3, 5, 1, 1, 3, 5,... Mẫu lặp lại này có độ dài là 4.
Vì vậy, ta có thể tính số dư khi chia 2023 cho 4
2023:4 dư 3
Vậy số hạng thứ 2023 sẽ tương ứng với số hạng thứ 3 trong mẫu lặp. Tính số dư khi chia 3 cho 8, ta được kết quả là 3.

Gọi 4 số hạng cần tìm lần lượt là a,b,c,d
Theo đề bài ta có:
\(\frac{a}{3}=\frac{b}{5};\frac{b}{4}=\frac{c}{6};\frac{c}{2}=\frac{d}{3}\)
=> \(\frac{a}{12}=\frac{b}{20};\frac{b}{20}=\frac{c}{30};\frac{c}{30}=\frac{d}{45}\)
=> \(\frac{a}{12}=\frac{b}{20}=\frac{c}{30}=\frac{d}{45}\) và a +b+ c+ d =321
Áp dụng t/c của dãy tỉ số = nhau ta có:
\(\frac{a}{12}=\frac{b}{20}=\frac{c}{30}=\frac{d}{45}=\frac{a+b+c+d}{12+20+30+45}=\frac{321}{107}=3\)
=> \(\left[\begin{matrix}a=3.12\\b=3.20\\c=3.30\\d=3.45\end{matrix}\right.\) => \(\left[\begin{matrix}a=36\\b=60\\c=90\\d=135\end{matrix}\right.\)
Vậy........................
Nguyễn Huy ThắngNguyễn Huy TúHoàng Thị Ngọc AnhNguyễn Hoàng ViệtNguyen Quang Trungsoyeon_Tiểubàng giảiTrần Việt LinhTrương Hồng HạnhNguyễn Thị Thu AnSilver bullet

B = 1 + (2 + 3 + 4 + ... + 98 + 99).
Ta thấy tổng trong ngoặc gồm 98 số hạng, nếu chia thành các cặp ta có 49 cặp nên tổng đó là:
(2 + 99) + (3 + 98) + ... + (51 + 50) = 49.101 = 4949
Khi đó B = 1 + 4949 = 4950

Tham khảo :Hai dạng toán nâng cao toán 7 dành cho học sinh giỏi toán
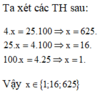
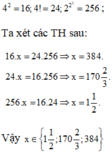
Gọi số hạng thứ nhất là a thì số hạng thứ hai là \(\dfrac{2}{5}\cdot a\), số hạng thứ ba là \(\dfrac{2}{5}\cdot a+\dfrac{7}{4}\), số hạng thứ tư là \(\dfrac{1}{5}\cdot a\).
Khi đó, ta được:
\(a+\dfrac{2}{5}\cdot a+\dfrac{2}{5}\cdot a+\dfrac{7}{4}+\dfrac{1}{5}\cdot a=\dfrac{57}{4}\\ \Leftrightarrow2a+\dfrac{7}{4}=\dfrac{57}{4}\\ \Leftrightarrow2a=\dfrac{50}{4}\\ \Leftrightarrow a=\dfrac{25}{4}\)
Vậy số hạng thứ nhất là \(\dfrac{25}{4}\), số hạng thứ hai là \(\dfrac{5}{2}\), số hạng thứ ba là \(\dfrac{17}{4}\), số hạng thứ tư là \(\dfrac{5}{4}\).
Ta được: \(14\dfrac{1}{4}=\dfrac{25}{4}+\dfrac{5}{2}+\dfrac{17}{4}+\dfrac{5}{4}\)