
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn D.
Nhóm thứ 5 là: [158;160)
Giá trị đại diện của nhóm thứ 5 là:
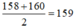

Đáp án D.
+ Điểm trung bình của 100 học sinh là: x = 15 , 09
+ Độ lệch chuẩn:
S = 1 100 2 . 9 - 15 , 09 2 + 1 . 10 - 15 , 09 2 + . . . + 3 . 19 - 15 , 09 2
S ≈ 2 , 17
Chú ý: Cách sử dụng máy tính bỏ túi
Bước 1: Vào chế độ thống kê:
![]()
Bước 2: Hiển thị cột tần số:
![]()
Bước 3: Nhập các giá trị: nhập lần lượt từng giá trị, nhập xong mỗi giá trị ấn phím ![]() để lưu vào máy.
để lưu vào máy.
Bước 4: Nhập tần số: Sau khi nhập đủ các giá trị, dùng phím ![]() để di chuyển con trỏ trở về đầu cột tần số.
để di chuyển con trỏ trở về đầu cột tần số.
Nhập lần lượt tần số tương ứng với mỗi giá trị.
Kết thúc ấn phím ![]() để thoát khỏi màn hình thống kê hai cột.
để thoát khỏi màn hình thống kê hai cột.
Bước 5: * Tính giá trị trung bình:
![]()
* Tính độ lệch chuẩn s:
![]()
(Tính phương sai s2 ta ấn tiếp phím ![]() )
)

a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
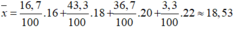
Số trung bình cộng của bảng 8 là:
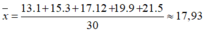
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ trung bình trong tháng 2 khoảng 0,6ºC.

5+5^2+.....+5^100 chia het cho 6
= (5+5^2)+(5^3+5^4)+..........+(5^99+5^100)
= (5.1+5.5)+(5^3.1+5^3.5)+.........+(5^99.1+5^99.5)
= 5.(1+5)+5^3.(1+5)+...........+5^99.(1+5)
= 5.6 + 5^3.6 + .............+5^99.6
= 6 .( 5+ 5^3+.............+ 5^99) chia hết cho 6
Vậy : 5+5^2+.....+5^100 chia het cho 6
cứ 2 số cạnh nhau thì chia hết cho 6. có 50 cặp như thế. vậy tổng chia het cho6

có
\(A=3\cdot11...111\cdot9\cdot11...111\)(100 số 1)
\(A=27\cdot\left(11...111\right)^2\)(100 số 1)
\(A=27\left(10^{99}+...+10^0\right)^2\)
\(A=27\left(\dfrac{10^{99+1}-1}{10-1}\right)^2\)
\(A=\dfrac{10^{200}-2\cdot10^{100}+1}{3}\)

Đặt \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}\)
\(B=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\)
Ta có: \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \)\(B=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\left(1\right)\)
Mà \(B=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{99\cdot100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}< 1\left(2\right)\). Từ \(\left(1\right)\) và \(\left(2\right)\) ta có:
\(A< B< 1\Rightarrow A< 1\)
C