K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 3 2021
\(y'=-3x^2+6x=0\Rightarrow\left[{}\begin{matrix}x=0\\x=2\end{matrix}\right.\)
Hàm đồng biến trên \(\left(0;2\right)\)

NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 3 2021
\(y'=x^2-2x+1=\left(x-1\right)^2\ge0\) ;\(\forall x\in R\)
\(\Rightarrow\) Hàm đồng biến trên R

CM
17 tháng 12 2017
Đáp án B
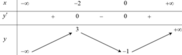
Từ bảng xét dấu f'(x) ta thấy trên khoảng ( - ∞ ; - 1 ) thì f'(x)<0 nên hàm số y=f(x) nghịch biến trên khoảng ( - ∞ ; - 1 )
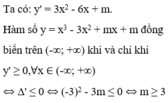

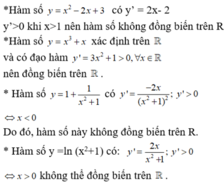

Lời giải:
\(y'=-3x^2+2mx=x(2m-3x)\)
\(y'=0\Leftrightarrow \left[\begin{matrix} x=0\\ x=\frac{2m}{3}\end{matrix}\right.\)
Nếu \(m=0\Rightarrow y'=-3x^2\leq 0\) (luôn nghịch biến- loại)
Nếu \(m>0\), lập bảng biến thiên suy ra:
$y$ đồng biến trên (1;2) khi và chỉ khi:
\(\frac{2m}{3}\geq 2\Leftrightarrow m\geq 3\)
Nếu \(m< 0\), lập bảng biến thiên suy ra hàm số chỉ đồng biến trên khoảng \((\frac{2m}{3};0)\) , tức là không thể đồng biến trên (1;2)
Vậy \(m\geq 3\)