Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
2 x + 3 x + 2 = x + m ⇔ 2 x + 3 = x 2 + m x + 2 x + 2 m ⇔ f x = x 2 + m x + 2 m - 3 = 0 ( 1 )
Rõ ràng f - 2 ≠ 0 , ∀ m nên ta cần có ∆ > 0 ⇔ m 2 - 4 2 m - 3 > 0 ⇔ [ m > 6 m < 2 .

Đáp án C
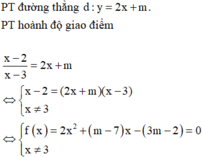
Để (C) cắt d tại 2 điểm phân biệt có hoành độ dương thì PT f(x) = 0 có 2 nghiệm dương phân biệt khác 3
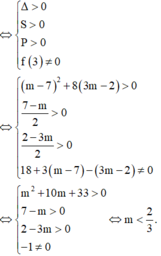

Chọn D.
Phương pháp:
Giải phương trình hoành độ giao điểm, tìm giao điểm của hai đồ thị.
Dựa vào công thức trọng tâm, xác định m.
Cách giải:
Phương trình hoành độ giao điểm của d và (C) là
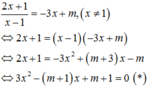
Để d cắt (C) tại hai điểm phân biệt A, B thì (*) có 2 nghiệm phân biệt khác 1
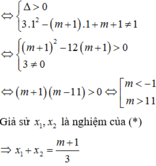


Đáp án A
Phương trình hoành độ giao điểm:
x 3 + 2 m x 2 + 3 ( m − 1 ) x+ 2 = − x+ 2 ⇔ x 3 + 2 m x 2 + ( 3 m − 2 ) x= 0 ⇔ x= 0 x 2 + 2 m x + ( 3 m − 2 ) = 0
+) Với m= -1 ba giao điểm là A 0 ; 2 , B 1 − 6 ; 1 + 6 , C 1 + 6 ; 1 − 6
MB = 16 + 4 6 ; MC = 16 − 4 6 ; BC = 4 3
Diện tích tam giác MBC=2 6
+) Với m= 4 ba giao điểm là A 0 ; 2 , B − 4 + 6 ; − 2 + 6 , C − 4 − 6 ; − 2 − 6
MB = 70 − 20 6 ; MC = 70 + 20 6 ; BC = 4 3
Diện tích tam giác MBC ≈ 9,1
Vậy m=-1



Đáp án đúng : C