Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp:
Xét tính đúng sai của các đáp án dựa vào các kiến thức hàm số đồng biến, nghịch biến trên khoảng xác định.
Cách giải:
*2 sai vì với c 1 < c 2 bất kỳ nằm trong a ; b ta chưa thể so sánh được f c 1 và f c 2
*3 sai. Vì y' bằng 0 tại điểm đó thì chưa chắc đã đổi dấu qua điểm đó. VD hàm số y = x 3
*4 sai: Vì thiếu điều kiện tại f ' x = 0 hữu hạn điểm.VD hàm số y = 1999 có y ' = 0 ≥ 0 nhưng là hàm hằng.
Chú ý khi giải:
HS thường nhầm lẫn:
- Khẳng định số 4 vì không chú ý đến điều kiện bằng 0 tại hữu hạn điểm.
- Khẳng định số 3 vì không chú ý đến điều kiện đổi dấu qua nghiệm.

Đáp án D
Ta có hàm số g x = f x - 2018 là hàm số bậc ba liên tục trên R.
Do a>0 nên l i m x → - ∞ g ( x ) = - ∞ ; l i m x → + ∞ g ( x ) = + ∞
Để ý g 0 = d - 2018 > 0 ; g 1 = a + b + c + d - 2018 < 0 nên phương trình g(x)=0 có đúng 3 nghiệm phân biệt trên R.
Khi đó đồ thị hàm số g x = f x - 2018 cắt trục hoành tại 3điểm phân biệt nên hàm số y = f x - 2018 có đúng 5 cực trị.

Phương trình mặt chắn của mặt phẳng (ABC) là: ![]()
Từ giả thiết 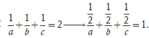 Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.
Kết hợp với a > 0, b > 0, c > 0 suy ra mặt phẳng (ABC) luôn đi qua một điểm cố định có tọa độ là
1
2
;
1
2
;
1
2
. Chọn C.

Đáp án D
Định lí: “Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho f c = 0 ”.
Mệnh đề 1: SAI ở giả thiết (a;b).
Mệnh đề 2: Nếu hàm số y=f(x) liên tục trên a ; b
và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho c hay f x = 0 là nghiệm của phương trình f(x)=0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì đồ thị hàm số y=f(x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f(x)=0 có nghiệm duy nhất trên (a;b). Do đó mệnh đề 3 ĐÚNG





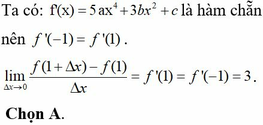

Đáp án C
Với a = b = 0,c > 0 thì y = c x + d ⇒ y ' = c > 0 , ∀ x ∈ ℝ nên hàm số đồng biến trên ℝ
Với a ≠ 0 , ta có YCBT ⇔ y ' = 3 a x 2 + 2 b x + c ≥ 0 , ∀ x ∈ ℝ
⇔ 3 a > 0 ∆ ' = b 2 - 3 a c ≤ 0 ⇔ a > 0 b 2 - 3 a c ≤ 0