
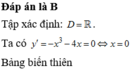

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

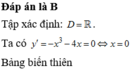



Đáp án A.
Đặt u = x 2 - 2 x , ta có y = f u ⇒ y ' = 2 x - 2 f ' u = 2 x - 2 f ' x 2 - 2 x .
Do đó, phương trình y ' = 0 ⇔ [ 2 x - 2 = 0 x 2 - 2 x = - 2 x 2 - 2 x = - 1 x 2 - 2 x = 0 ⇔ [ x - 1 3 = 0 x 2 - 2 x + 2 = 0 x 2 - 2 x = 0 ⇔ [ x = 0 x = 1 x = 2 .
Vậy hàm số đã chốc 3 điểm cực trị là x = 0; x= 1; x = 2.

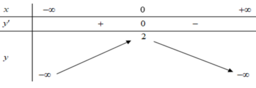
Đáp án D
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]

Đáp án B
Phương pháp: Đạo hàm của hàm hợp : ![]()
Tìm số nghiệm của phương trình y’ = f’(x2 – 2x) = 0
Cách giải:
![]()
![]()
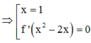
Vì f(x) liên tục trên R và có đúng ba điểm cực trị là –2; –1; 0 nên f’(x) đổi dấu tại đúng ba điểm –2; –1; 0 và f’(–2) = f’(–1) = f(0) = 0
Giải các phương trình:
![]() : vô nghiệm
: vô nghiệm
![]()
![]()

Như vậy, y’ = 0 có 3 nghiệm x = 0;1;2 và y’ đều đổi dấu tại 3 điểm này. Do đó, hàm số y = f(x2 – 2x) có 3 điểm cực trị

Đáp án A
Mệnh đề 1) sai vì f ' x 0 = 0 chỉ là điều kiện cần chưa là điều kiện đủ để hàm số đạt cực trị tại x 0
Mệnh đề 2) Sai vì khi f ' x 0 = f ' ' x 0 = 0 có thể hàm số có thể đạt cực trị hoặc không đạt cực trị tại x 0 .
Mệnh đề 3) sai vì f ' x đổi dấu qua điểm x 0 thì điểm x 0 có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.
Mệnh đề 4) Sai vì trong trường hợp này x 0 là điểm cực tiểu của đồ thị hàm số.

Đáp án A
A sai vì hàm số y = x 3 có y ' 0 = 0 nhưng không đạt cực trị tại x = 0
B sai vì hàm số y = x 4 có y ' 0 = 0 , y ' ' 0 = 0 đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = f ' ' x 0 = 0 thì điểm x 0 nhưng không đạt cực trị tại x = 0
C sai vì “Nếu f ' x đổi dấu khi x qua x 0 thì điểm x 0 là điểm trị (cực đại và cực tiểu) của hàm số y = f ' ' x
D sai vì “Nếu hàm số y = f x có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thoả mãn điều kiện f ' x 0 = 0 ; f ' ' x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f ' ' x