Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lò xo bị nén rồi lại buông tay nên \(\overrightarrow{F_1}=-\overrightarrow{F_2}\).
\(\Rightarrow F_1=F_2\Rightarrow m_1\cdot a_1=m_2\cdot a_2\Rightarrow\dfrac{m_1}{m_2}=\dfrac{a_2}{a_1}\)
Mặt khác: \(S=\dfrac{1}{2}at^2\Rightarrow a=\dfrac{2S}{t^2}\)
Từ đó: \(\dfrac{m_1}{m_2}=\dfrac{a_2}{a_1}=\dfrac{\dfrac{2S_2}{t^2}}{\dfrac{2S_1}{t^2}}=\dfrac{S_2}{S_1}=\dfrac{6}{2}=3\)
\(\Rightarrow m_1=3m_2=3\cdot2=6kg\)
Chọn A.

Áp dụng định luật hai Newton lên vật m1
\(\overrightarrow{F_1}+\overrightarrow{N_1}+\overrightarrow{P_1}=m_1\overrightarrow{a_1}\)
\(\Rightarrow F_1=m_1a_1\)
Áp dụng định luật hai Newton lên vật m2
\(\overrightarrow{F_2}+\overrightarrow{N_2}+\overrightarrow{P_2}=m_2\overrightarrow{a_2}\)
\(\Rightarrow F_2=m_2a_2\)
Lại có: \(F_1=F_2\Rightarrow m_1a_1=m_2a_2\)
Mà \(a=\dfrac{2s}{t^2}\)
\(\Rightarrow m_1s_1=m_2s_2\)
\(\Leftrightarrow m_1=3m_2\) (1)
Có: \(m_1+m_2=3\) (2)
Từ (1) và (2) giải hệ phương trình ta được: \(\left\{{}\begin{matrix}m_1=3\left(kg\right)\\m_2=1\left(kg\right)\end{matrix}\right.\)

Chọn D.
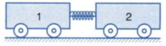
Gọi F 12 ⇀ là lực mà thông qua lò xo, xe (1) tác dụng lên xe (2).
Theo định luật II Niuton:
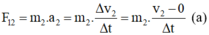
F 21 ⇀ là lực mà thông qua lò xo, xe (2) tác dụng lên xe (1).
Theo định luật II Niuton:
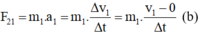
Theo định luật III Niuton, về độ lớn: F 12 = F 21 (c)
Từ (a), (b) và (c) suy ra:
m 2 v 2 ∆ t = m 1 v 1 ∆ t ⇒ m 2 = v 1 v 2 m 1 = 600 g
Vậy khối lượng xe lăn (2) là m2 = 600g.
Quãng đường xe A đi được là:
s A = v 0 t + 1 2 a 1 t 2 = 1 2 a 1 t 2 = 1
Quãng đường xe B đi được là:
s B = v 0 t + 1 2 a 2 t 2 = 1 2 a 2 t 2 = 2
Xét tỉ số: s A s B = a 1 a 2 = 1 2
Sử dụng định luật II Niuton ta có: m = F a
Mà theo định luật III Niuton ta có: FA=FB
→ m 1 m 2 = a 2 a 1 = 2
Vậy tỉ số khối lượng của xe A và B là 2
Đáp án: A