Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
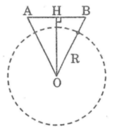
Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
Suy ra: HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
O A 2 = A H 2 + O H 2
Suy ra: O H 2 = O A 2 - A H 2
Suy ra:
OH = 
≈ 6508 (km)
Vì OH > R nên hai vệ tinh nhìn thấy nhau.
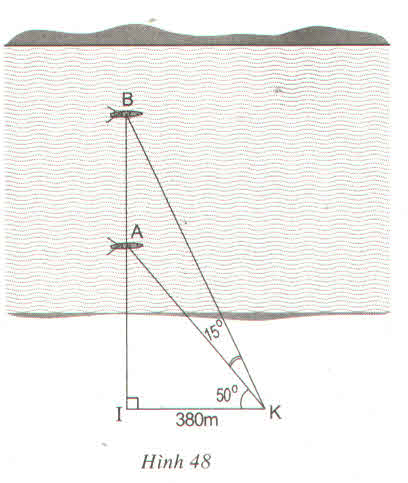
Gọi C là vị trí của máy bay.
Kẻ CH⊥ABCH⊥AB
Trong tam giác vuông ACH, ta có:
AH=CH.cotgˆA(1)AH=CH.cotgA^(1)
Trong tam giác vuông BCH, ta có:
BH=CH.cotgˆB(2)BH=CH.cotgB^(2)
Từ (1) và (2) suy ra:
(AH+BH)=CH.cotgˆA+CH.cotgˆB(AH+BH)=CH.cotgA^+CH.cotgB^
Suy ra:
CH=ABcotgˆA+cotgˆB=ABcotg40∘+cotg30∘≈102,606(cm)
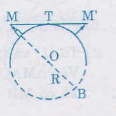
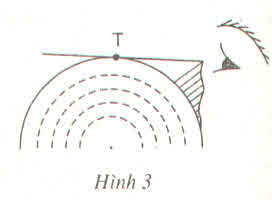
Áp dụng kết quả bài tập 34 ta có:
MT2 = MA. MB
MT2 = MA.(MA + 2R)
Thay số vào đẳng thức trên và lấy đơn vị là km, ta có:
MT2 = 0,04 (0,04 + 12.800)
MT ≈ 23 (km)
Cũng tương ta có;
MT2 = 0,01(0,01 +12.800)
MT ≈ 11 (km)
Từ đó: MM' = MT + M'T = 23+11= 34(km)
Vậy khi ngọn hải đăng khoảng 34 km thì người thủy thủ bắt đầu trông thấy ngọn hải đăng.
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
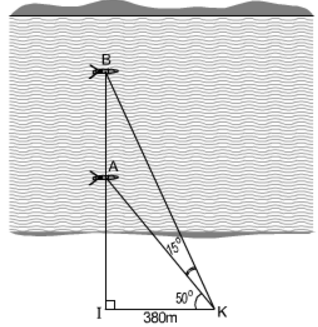
Độ cao của máy bay là CD, độ dài AB = 60m; D A C ^ = 30 0 ; D B C ^ = 50 0
Gọi BC = x => AC = 60 + x
Xét tam giác BDC vuông tại C có:
Xét tam giác ADC vuông tại C có:
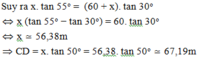
Vậy độ cao của máy bay so với mặt đất là 67,19m
Đáp án cần chọn là: C
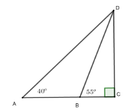
Độ cao của máy bay là CD, độ dài AB = 80m
Gọi BC = x (x > 0) => AC = 80 + x
Xét tam giác BDC vuông tại C có CD = x . tan 55 0
Xét tam giác ADC vuông tại C có CD = (80 + x). tan 44 0
Suy ra x . tan 55 0 = (80 + x). tan 44 0
=> x ≈ 113,96m
=> CD = 113,96. tan 55 0 ≈ 162,75m
Vậy độ cao của máy bay so với mặt đất là 162,75m
Đáp án cần chọn là: A
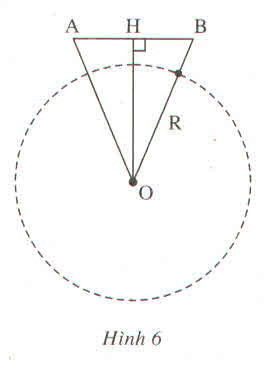
Vì hai vệ tinh cùng cách mặt đất 230 km nên tam giác AOB cân tại O.
Ta có: OA = R + 230
= 6370 + 230 = 6600 (km)
Trong tam giác AOB ta có: OH ⊥ AB
\(\Rightarrow\): HA = HB = AB/2 = 2200/2 = 1100 (km)
Áp dụng định lí Pi-ta-go vào tam giác vuông AHO, ta có:
OA2 = AH2 + OH2
\(\Rightarrow\): OH2 = OA2 – AH2
\(\Rightarrow\) :OH =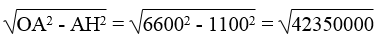
≈ 6508 (km)
Vì OH > R nên hai vệ tinh nhìn thấy nhau.