Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi t1,t2 lần lượt là thời gian vật 1, vật 2 rơi đến khi chạm đất
Ta có: t12=\(\dfrac{2s_1}{g}\)
\(\Rightarrow\)g=\(\dfrac{2s_1}{t_1^2}\)
Lại có: v1=g.t1
\(\Rightarrow\) t1=\(\dfrac{v_1}{g}=\dfrac{v_1.t_1^2}{2s_1}\)
\(\Leftrightarrow t_1=\dfrac{2s_1}{v_1}\)
Mặt khác:
t22=\(\dfrac{2s_2}{g}\)
\(\Rightarrow\)g=\(\dfrac{2s_2}{t_2^2}\)
Ta có: v2=g.t2=\(\dfrac{2s_2}{t_2^2}\)t2=\(\dfrac{2s_2}{t_2}=\dfrac{2s_2}{3.t_1}=\dfrac{2s_2}{3.\dfrac{2s_1}{v_1}}=\dfrac{s_2v_1}{3s_1}\)
Vậy vận tốc của vật thứ hai khi chạm đất là: \(\dfrac{s_2v_1}{3s_1}\)

Thời gian rơi của vật 1:
\(t_1=\sqrt{\dfrac{2h_1}{g}}\)
Thời gian rơi của vật 2:
\(t_2=\sqrt{\dfrac{2h_2}{g}}\)
Vì thời gian rơi của vật 1 bằng nửa thời gian rơi của vật 2:
\(\Rightarrow t_1=\dfrac{1}{2}t_2\Rightarrow\dfrac{t_1}{t_2}=2\)
\(\Rightarrow\dfrac{\sqrt{\dfrac{2h_1}{g}}}{\sqrt{\dfrac{2h_2}{g}}}=2\Rightarrow\sqrt{\dfrac{h_1}{h_2}}=2\Rightarrow\dfrac{h_1}{h_2}=4\)

1. Thả một hòn sỏi rơi tự do từ độ cao s xuống đất, trong giây cuối cùng trước khi chạm đất hòn sỏi rơi được quảng đường 15m. Lấy g=10ms2. Độ cao h thả sỏi là?
Trả lời :
Quãng đường vật đi đc đến khi chạm đất là :
\(h=\dfrac{1}{2}.g.t^2=5.t^2\)
Quãng đường vật đi đc trước khi chạm đất 1s là :
\(h'=\dfrac{1}{2}.g.\left(t-1\right)^2=5.\left(t-1\right)^2\)
Thời gian thả sỏi : \(5t^2-5\left(t-1\right)^2=15\)
=> t=2s
Độ cao h thả sỏi là :
h-h'=15
=> h=20m
Gọi v12 là vận tốc của cano so với nước
v23 là vận tốc nước so với bờ
v13 là vận tốc cano so với bờ khi xuôi dòng
Ta có: Vận tốc cano so với bờ khi ngược dòng
v13=\(-\dfrac{-15}{1}=15\)km/h
Vận tốc của cano so với nước là:
v23= v13+v12=15+2=17km/h
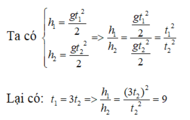
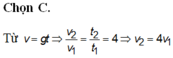
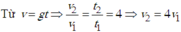
Đáp án D