Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1/2.m v 2 m a x = mgl(1 - cos α 0 )
![]()
F - mg = m v 2 m a x /l ⇒ F = m(g + v 2 m a x /l)
F = 0,05(9,8 + 2 , 3 2 /2) ≈ 0,62N

Ban đầu t = 0 thì x = 2 cm, lúc này vật đang ở biên độ dương.
Quả cầu dao động được nửa chu kì thì x = -2 cm (vật ở biên độ âm)
Chiều dài của lò xo: \(\ell=\ell_0+\Delta\ell_0+x=40+10-2=48(cm)\)

Theo giả thiết thì hai bản tụ đặt thẳng đứng trái dấu, nên ta có hình sau:
+ + + + + - - - - - α E P F T
Góc lệch ở VTCB: \(\tan\alpha=\frac{F}{P}=\frac{qE}{mg}=\frac{qU}{mgd}=\frac{10^{-5}.400}{0,01.10.0,1}=0,4\)
\(\Rightarrow\alpha=21,8^0\)

Động năng ban đầu cực đại của quang electron bứt ra từ mặt quả cầu:
\(\frac{mv^2_{max}}{2}=\frac{hc}{\lambda}-A=2,7.10^{-19}J\)
Gọi Q là điện tích của quả cầu, điện tích này phải là điện tích dương để giữ electron; điện tích Q phân bố đều trên mặt quả cầu, do đó điện thế trên mặt quả cầu là:
\(V=9.10^9.\frac{Q}{R}\). Trên quả cầu hình thành điện trường với các đường sức vuông góc với mặt cầu và hướng ra ngoài ( vì Q>0), điện trường này ngăn cản electron thoát ra khỏi quả cầu, công của điện trường cản là: \(W=eV=9.10^9.\frac{Qe}{R}\)
Muốn cho electron không thoát ra , công đó phải bằng động năng ban đầu cực đại của electron nghĩa là: \(9.10^9.\frac{Qe}{R}=\frac{mv^2_{max}}{2}\)
Thay số ta rút ra : \(Q=1,9.10^{-11}C\)
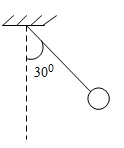

Các lực tác dụng lên vật
+ Trọng lực P → (thẳng đứng hướng xuống)
+ Lực điện F → d (hai điện tích giống nhau nên hai điện tích đẩy nhau)
+ Lực căng T →
+ Khi quả cầu cân bằng ta có: T → + F → + P → = 0
+ Từ hình vẽ ta có: tan α = F P
Chọn đáp án C