Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dung quy tắc hợp lực song song: \(\frac{F_1}{F_2}=\frac{d_2}{d_1}=\frac{40}{60}=\frac{2}{3}\)(1)
Mà \(F_1+F_2=P=1000N\) (2)
Từ (1) và (2) suy ra \(\begin{cases}F_1=400N\\F_2=600N\end{cases}\)

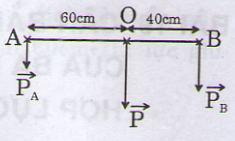
Áp dụng quy tắc hợp lực song song cùng chiều.
Ta có: P= PA + PB = 1000N (1)
Mặt khác: PA. OA = PB. OB
=> =
=
=
(2)
(1) & (2) => PA = 600N và PB= 400N

Chọn B.
Gọi F1, F2 là độ lớn của hai lực đặt lên hai đầu của cái gậy. F1, F2 lần lượt cách vai là d1 = 60 cm, d2 = 40 cm.
Ta có: F1 + F2 = mg = 1000 (1)
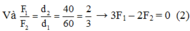
Từ (1) và (2) → F1 = 400 N, F2 = 600 N.

Chọn B.
Gọi F 1 , F 2 là độ lớn của hai lực đặt lên hai đầu của cái gậy. F1, F2 lần lượt cách vai là d 1 = 60 cm, d 2 = 40 cm.
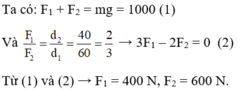

Gọi \(F_1;F_2\) lần lượt là các lực mà vai của người thứ nhất và hai chịu.
Theo quy tắc Momen lực ta có:
\(d_1\cdot F_1=d_2\cdot F_2\)
\(\Rightarrow60\cdot F_1=40\cdot F_2\left(1\right)\)
Mà \(F_1+F_2=1000\left(2\right)\)
Từ (1|) và (2) \(\Rightarrow\left\{{}\begin{matrix}F_1=400N\\F_2=600N\end{matrix}\right.\)
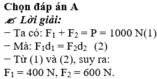

Gọi P1 là lực tác dụng lên vai người đi trước, P2 là lực tác dụng lên vai người đi sau, ta đã có: d1 = OO1 = 60 cm; d2 = OO2 = 40 cm.
Áp dụng quy tắc hợp lực hai lực song song cùng chiều ta được:
Giải hệ (1) và (2) ta được: P1 = 400 N, P2 = 600 N