Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Thời gian người đó đi quãng đường AB:
8 giờ 45 phút - 6 giờ 15 phút = 2 giờ 30 phút = 2,5 giờ
Vận tốc trung bình của ô tô:
$120:2,5=48$ (km/h)

Đáp án B.
Gọi x (phút) là thời gian mà bạn A đến chờ ở thư viện.
Gọi y (phút) là thời gian mà bạn B đến chờ ở thư viện.
Điều kiện: ![]()
![]() (là diện tích hình vuông cạnh 60)
(là diện tích hình vuông cạnh 60)
Điều kiện gặp nhau là
![]() (*)
(*)
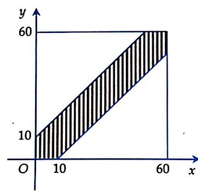
Do điểm ![]() thỏa điều kiện (*) thuộc lục giác gạch sọc giới hạn bởi 2 đường thẳng
thỏa điều kiện (*) thuộc lục giác gạch sọc giới hạn bởi 2 đường thẳng ![]() là hình vuông của không gian mẫu.
là hình vuông của không gian mẫu.
Lục giác có diện tích
![]()
Vậy xác suất để 2 người gặp nhau là:
![]()

Ta có:
+ Công thức tính lương của phương án thứ nhất: \({S_n} = 120 + \left( {n - 1} \right).18\)
+ Công thức tính lương của phương án thứ hai: \({Q_n} = 24 + \left( {n - 1} \right).1,8\)
a) Sau ba năm:
- Phương án thứ nhất có: \({S_3} = 120 + \left( {3 - 1} \right).18 = 156\) (triệu đồng)
- Phương án thứ hai có: \({Q_{12}} = 24 + (12 - 1).1,8 = 43,8\) (triệu đồng)
Nếu kí hợp đồng lao động 3 năm, em sẽ chọn phương án thứ nhất
b) Sau 10 năm:
- Phương án thứ nhất có: \({S_{10}} = 120 + \left( {10 - 1} \right).18 = 282\) (triệu đồng)
- Phương án thứ hai có: \({Q_{40}} = 24 + (40 - 1).1,8 = 94,2\) (triệu đồng)
Nếu kí hợp đồng lao động 10 năm, em sẽ chọn phương án thứ nhất.

Tham khảo:
a) Số xe trung bình đi qua trạm thu phí trong mỗi phút là: \(\bar x \approx 17,4\) (xe).
b)

c) Do số xe là số nguyên nên ta hiệu chỉnh lại như sau:

Số xe trung bình đi qua trạm thu phí trong mỗi phút từ bảng tần số ghép nhóm là:
\(\bar x = \frac{{5.8 + 9.13 + 3.18 + 9.23 + 4.28}}{{30}} \approx 17,7\)

Đáp án C
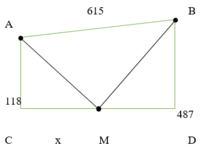
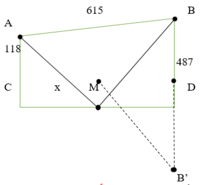
Cách 1: Giải bằng hàm số
Đặt CM = x (x > 0)
Dễ tính ra CD ![]()
Từ đề bài ta có: f (x) = ![]()
Quãng đường ngắn nhất người đó có thể đi
⇔ Giá trị nhỏ nhất của f(x) trên (0;492)
Ta có: f’(x) = 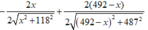
=> f’(x) = 0
![]()
![]()
![]()
![]()
![]()
Ta có bảng biến thiên
| x |
0 |
0 |
492 |
| y’ |
|
+ 0 - |
|
| y |
779,8 |
||
Vậy quãng đường ngắn nhất mà người đó có thể đi là: 779,8
Cách 2: Giải bằng hình học
Gọi B’ là điểm đối xứng của B qua D
Dễ thấy AM + MB = AM + MB’
⇔ AM + MB ngắn nhất
⇔ AM + MB’ ngắn nhất
Dễ thấy theo bất đẳng thức tam giác: AM + MB’ ≥ AB’
⇔ AM + MB’ ngắn nhất ó AM + MB’ = AB’
Dấu “=” xảy ra khi và chỉ khi A, M, B’ thẳng hàng