Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cả 2 người thợ làm cùng nhau mỗi giờ làm được
\(\dfrac{1}{4}+\dfrac{1}{6}=\dfrac{5}{12}\)( Công việc )
Cả 2 người thợ làm chung thì hoàn thành công việc sau
\(1:\dfrac{5}{12}=\dfrac{12}{5}=24h\)
Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x,y
Theo đề, ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{4}{x}+\dfrac{6}{y}=\dfrac{5}{12}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{24}\\\dfrac{1}{y}=\dfrac{1}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=24\end{matrix}\right.\)

Gọi thời gian người thứ nhất làm riêng xong công việc là x(giờ)
Gọi thời gian người thứ hai làm riêng xong công việc là y(giờ)
Điều kiện: x; y > 0
Trong 1 giờ người thứ nhất làm được 1/x (công việc)
Trong 1 giờ người thứ hai làm được 1/y (công việc)
Vì hai người làm chung trong 15 giờ được 1/6 công việc nên ta có phương trình:
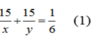
Vì người thứ nhất làm một mình trong 12 giờ và người thứ hai làm một mình trong 20 giờ được 1/5 công việc nên ta có phương trình:
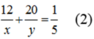
Từ (1) và (2) ta có hệ phương trình:

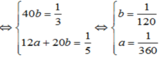
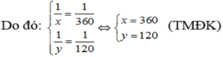
Vậy người thứ nhất làm riêng xong công việc trong 360 giờ; người thứ hai làm riêng xong công việc trong 120 giờ.

Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x(giờ),y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1 giờ, người thứ nhất làm được \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được \(\dfrac{1}{16}\left(côngviệc\right)\)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\left(1\right)\)
Trong 15 giờ thì người thứ nhất làm được \(\dfrac{15}{x}\)(công việc)
Trong 6 giờ thì người thứ hai làm được \(\dfrac{6}{y}\)(công việc)
Nếu người thứ nhất làm trong 15 giờ và người thứ hai làm trong 6 giờ thì hai người làm được 75% công việc nên ta có:
\(\dfrac{15}{x}+\dfrac{6}{y}=75\%=\dfrac{3}{4}\)
=>\(\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{5}{y}=\dfrac{5}{16}\\\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{y}=\dfrac{5}{16}-\dfrac{1}{4}=\dfrac{1}{16}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=48\\\dfrac{1}{x}=\dfrac{1}{16}-\dfrac{1}{48}=\dfrac{1}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\left(nhận\right)\)
Vậy: Để hoàn thành xong công việc khi làm một mình thì người thứ nhất cần 24 giờ, còn người thứ hai cần 48 giờ

Gọi thời gian làm xong việc một mình của người thứ nhất và người thứ hai lần lượt là \(x,y\left(x,y>0\right)\)(đơn vị: h)
Trong 1 giờ, người thứ nhất làm xong \(\frac{1}{x}\)công việc còn người thứ hai làm xong \(\frac{1}{y}\)công việc.
2 người cùng làm trong 12 giờ thì xong công việc nên ta có phương trình \(\frac{12}{x}+\frac{12}{y}=1\)(1)
Trong 8 giờ, 2 người hoàn thành \(\frac{8}{x}+\frac{8}{y}\)công việc, sau đó người thứ 2 làm việc một mình trong 6h40p \(=\frac{20}{3}\)h, tức là hoàn thành thêm \(\frac{20}{3y}\) công việc thì xong công việc nên ta có pt \(\frac{8}{x}+\frac{8}{y}+\frac{20}{3y}=1\)(2)
Từ (1) và (2) ta có hpt \(\hept{\begin{cases}\frac{12}{x}+\frac{12}{y}=1\\\frac{8}{x}+\frac{8}{y}+\frac{20}{3y}=1\end{cases}}\)
Đặt \(\hept{\begin{cases}\frac{1}{x}=a\left(a>0\right)\\\frac{1}{y}=b\left(b>0\right)\end{cases}}\), hpt trên trở thành \(\hept{\begin{cases}12a+12b=1\\8a+8b+\frac{20}{3}b=1\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}24a+24b=2\\24a+24b+20b=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}12a+12b=1\\20b=1\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}12a+12.\frac{1}{20}=1\\b=\frac{1}{20}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}a=\frac{1}{30}\\b=\frac{1}{20}\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}\frac{1}{x}=\frac{1}{30}\\\frac{1}{y}=\frac{1}{20}\end{cases}}\Leftrightarrow\hept{\begin{cases}x=30\\y=20\end{cases}}\)(nhận)
Vậy người thứ nhất làm một mình xong công việc mất 30h, người thứ hai làm xong công việc một mình mất 20h

Gọi thời gian làm 1 mình xong công việc của 2 người thợ lần lượt là x>0 và y>0 giờ
Trong 1h hai người lần lượt làm được: \(\dfrac{1}{x}\) và \(\dfrac{1}{y}\) phần công việc
Do đó ta có pt: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\)
Trong 8h người thứ nhất làm được: \(\dfrac{8}{x}\) phần công việc
Trong 6h người thứ 2 làm được: \(\dfrac{6}{y}\) phần công việc
Ta có pt: \(\dfrac{8}{x}+\dfrac{6}{y}=\dfrac{2}{5}\) (với \(\dfrac{2}{5}=40\%\))
Từ đó ta có hệ: \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{18}\\\dfrac{8}{x}+\dfrac{6}{y}=\dfrac{2}{5}\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}=\dfrac{1}{30}\\\dfrac{1}{y}=\dfrac{1}{45}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=45\end{matrix}\right.\)

Công suất làm việc mỗi giờ của người thứ nhất, người thứ hai lần lượt là a,b (a,b>0)
Ta lập hpt:
\(\left\{{}\begin{matrix}4a+4b=1\\a+2b=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{6}\\b=\dfrac{1}{12}\end{matrix}\right.\)
Vậy nếu làm một mình người thứ nhất cần 6 giờ để hoàn thành công việc, người thứ hai cần đến 12 giờ để hoàn thành công việc đó.
dạ mink có lớp 5