Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
24 gio thi xong
bai nay lop 5
tk minh nha
happy new year
Nhưng bài này là giải bài toán bằng cách lập hệ phương trình, không phải giải theo cấp 1
Gọi thời gian để người thứ nhất, người thứ hai làm xong công việc lần lượg là x, y (giờ; x, y \(\in\) N*)
Khi đó trong mỗi giờ người thứ nhất làm được \(\dfrac{1}{x}\) công việc, người thứ hai làm được \(\dfrac{1}{y}\) công việc.
Theo bài ra ta có: \(\left\{{}\begin{matrix}\dfrac{16}{x}+\dfrac{16}{y}=1\\\dfrac{3}{x}+\dfrac{6}{y}=\dfrac{1}{4}\end{matrix}\right.\).
Giải ra ta có \(\dfrac{1}{x}=\dfrac{1}{24};\dfrac{1}{y}=\dfrac{1}{48}\Rightarrow x=24;y=48\) (TMĐK)
Vậy....
Gọi x ( giờ ) là thời gian hoàn thành công việc một mình của người thứ nhất
y ( giờ ) là thời gian hoàn thành công việc một mình của người thứ hai
( x , y > 0 )
Năng suất ⇒thứ nhất là : \(\dfrac{1}{x} \) ( công việc/giờ )
Năng suất người thứ hai là : \(\dfrac{1}{y}\) ( công việc/ giờ )
Vì hai người làm chung một công việc thì sau 16 giờ làm xong nên ta có pt : \(( \dfrac{1}{x} + \dfrac{1}{y} ).16 = 1 \) ⇒ \(\dfrac{16}{x} + \dfrac{16}{y} = 1 \) ( công việc ) (1)
Vì người thứ nhất làm một mình trong 3 giờ và người thứ hai làm một mình trong 6 giờ thì cả hai người làm được 1/4 công việc nên :
\(\dfrac{3}{x} + \dfrac{6}{y} = \dfrac{1}{4}\) ( công việc ) (2)
Từ (1) , (2) => \(\begin{cases} \dfrac{16}{x} + \dfrac{16}{y} = 1\\ \dfrac{3}{x} + \dfrac{6}{y} = \dfrac{1}{4} \end{cases} \) => \(\begin{cases} x = 24 \\ y = 48 \end{cases} \) (n)
Vậy.... ( cách 1 )
Công suất làm việc mỗi giờ của người thứ nhất, người thứ hai lần lượt là a,b (a,b>0)
Ta lập hpt:
\(\left\{{}\begin{matrix}4a+4b=1\\a+2b=\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{1}{6}\\b=\dfrac{1}{12}\end{matrix}\right.\)
Vậy nếu làm một mình người thứ nhất cần 6 giờ để hoàn thành công việc, người thứ hai cần đến 12 giờ để hoàn thành công việc đó.
Gọi thời gian người thứ nhất và người thứ hai hoàn thành công việc khi làm một mình lần lượt là x(giờ),y(giờ)
(Điều kiện: x>0 và y>0)
Trong 1 giờ, người thứ nhất làm được \(\dfrac{1}{x}\)(công việc)
Trong 1 giờ, người thứ hai làm được \(\dfrac{1}{y}\)(công việc)
Trong 1 giờ, hai người làm được \(\dfrac{1}{16}\left(côngviệc\right)\)
Do đó, ta có phương trình: \(\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\left(1\right)\)
Trong 15 giờ thì người thứ nhất làm được \(\dfrac{15}{x}\)(công việc)
Trong 6 giờ thì người thứ hai làm được \(\dfrac{6}{y}\)(công việc)
Nếu người thứ nhất làm trong 15 giờ và người thứ hai làm trong 6 giờ thì hai người làm được 75% công việc nên ta có:
\(\dfrac{15}{x}+\dfrac{6}{y}=75\%=\dfrac{3}{4}\)
=>\(\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\left(2\right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\\\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{x}+\dfrac{5}{y}=\dfrac{5}{16}\\\dfrac{5}{x}+\dfrac{2}{y}=\dfrac{1}{4}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{y}=\dfrac{5}{16}-\dfrac{1}{4}=\dfrac{1}{16}\\\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{16}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=48\\\dfrac{1}{x}=\dfrac{1}{16}-\dfrac{1}{48}=\dfrac{1}{24}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=24\\y=48\end{matrix}\right.\left(nhận\right)\)
Vậy: Để hoàn thành xong công việc khi làm một mình thì người thứ nhất cần 24 giờ, còn người thứ hai cần 48 giờ
Gọi người 1 , 2 làm trong k , t ngày thì xong công việc ( k,t>0 )
Ta có hệ pt \(\int^{\frac{2}{k}+\frac{5}{t}=\frac{1}{2}}_{\frac{3}{k}+\frac{3}{t}=1-\frac{1}{20}}\)
Đáp án A
Gọi thời gian người thợ thứ nhất làm một mình xong việc là x(giờ) (x > 16)
Thời gian người thợ thứ hai làm một mình xong việc là y(giờ) (y > 16)
Suy ra trong thời gian 1 giờ người thợ thứ nhất làm được 1/x công việc
Trong thời gian 3 giờ người thợ thứ nhất làm được 3/x công việc
Trong thời gian 1 giờ người thợ thứ hai làm được 1/y công việc
Trong thời gian 6 giờ người thợ thứ hai làm được 6/y công việc
Hai người cùng làm trong 16 giờ thì xong việc, nên 1 giờ cả 2 người làm được 1/16 ta có phương trình:
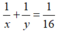
Người thứ nhất làm 3 giờ và người thứ hai làm 6 giờ thì được một phần tư công việc, ta có phương trình:
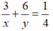
Từ đó ta có hệ phương trình:
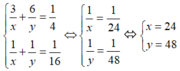
Kết luận: thời gian người thợ thứ nhất làm một mình xong việc là 24 (giờ)
Thời gian người thợ thứ hai làm một mình xong việc là 48 giờ