Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\lambda = v/f = 0.8/100 = 0.008m = 0.8cm.\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{0}{\lambda}-\frac{0}{2\pi})| = |2a| = 2a.\)
\(u_M = A_M\cos(2\pi ft - \pi\frac{d_2+d_1}{\lambda}+\frac{\varphi_1+\varphi_2}{2})\\= A_M\cos(200\pi t - \pi\frac{8+8}{0.8}+\frac{0}{2})= 2a\cos(200\pi t - \pi\frac{8+8}{0.8})= 2a\cos(200\pi t-20\pi)=2a\cos(200\pi t)\)

Chọn đáp án B
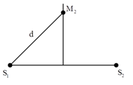
gọi d2 là khoảng cách từ s1 tới M2. Ta có d2-d1=k. lamda. M1M2 ngắn nhất khi k=+ -1.
Với k=+1. thì d2=d1+lamda=8,8cm
M1M2 = 7,84 – 6,93 = 0,91cm
Tương tự, với k=-1, đc M1M2=0,94cm.
Vậy đáp án B ( Chọn số nhỏ hơn)

Khi hệ vân giao thoa đã ổn định thì trung điểm I của S 1 S 2 lại luôn luôn là cực đại giao thoa. Do đó, ta phải có :
S 1 I = S 2 I = k λ /2 + λ /4 = (2k + 1) λ /4
S 1 S 2 = 2 S 1 I = (2k + 1) λ /2
Ban đầu ta đã có : S 1 S 2 = 8cm = 10 λ = 20 λ /2
Vậy chỉ cần tăng khoảng cách S 1 , S 2 thêm λ /2 tức là 0,4 cm.
Khi đó nếu không kể đường trung trực của S 1 S 2 thì có 20 gợn sóng hình hypebol (vì gợn sóng là quỹ tích những điểm dao động mạnh hơn cả).

Nếu tính toán liên quan đến 1 dao động của 1 điểm thì 2 phương trình đó là như nhau.
Nhưng trong giao thoa sóng, hay truyền sóng thì cần phải viết là Um=2acos(200pit-20pi) để thể hiện điểm này dao động trễ pha so với nguồn là bao nhiêu.

\(\lambda = v/f = 80/20 = 4cm.\)
\(\triangle \varphi = \pi-0=\pi.\)
Nhận xét: \(BM-AM=(BI+IM)-(AI-IM)=2MI\)
\( A_M = |2a\cos\pi(\frac{d_2-d_1}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{BM-AM}{\lambda}-\frac{\triangle\varphi}{2\pi})|\\=|2a\cos\pi(\frac{2MI}{\lambda}-\frac{\triangle\varphi}{2\pi})| = |2a\cos\pi(\frac{6}{4}-\frac{\pi}{2\pi})| = |-2a|=2a=10 mm.\)

Chọn đáp án B
x A M = A c os ( ω t − 2 π d 1 λ ) x B M = A cos ( ω t + π − 2 π d 1 λ )
phương trình sóng tại M
x M = x A M + x B M = − 2 A sin d 2 + d 1 λ . sin ( ω t − d 2 + d 1 λ π )
Biên độ sóng tại M: A M = 2 A sin d 2 − d 1 λ π ; tại M nếu A M = A 2
⇒ sin d 2 − d 1 λ π = ± 1 2 ⇒ d 2 − d 1 λ π = π 4 + k π 2 ⇒ d 2 − d 1 = λ 4 + k λ 2
Xét trên AB
d 2 A − d 1 A ≤ d 2 − d 1 ≤ d 2 B − d 1 B ⇔ − A B ≤ λ 4 + k λ 2 ≤ A B
Ta có: f = ω 2 π = 10 H z ; λ = v t = 3 c m
⇒ − 20,5 ≤ k ≤ 19,5 ⇒ k = 0, ± 1, ± 2... ± 19, − 20
⇒ có 40 điểm.

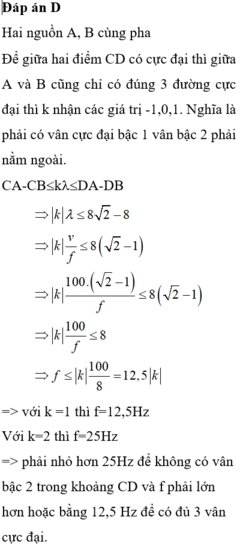
Ta có : λ = v/f = 80/100 = 0,8cm và d 1 = d 2 = d = 8cm.
Theo Bài 8 (SGK Vật lí 12), ta có :
d 1 + d 2 = 16cm = 20 λ d 2 - d 1 = 0
ta được : u M 1 = 2Acos(200 π t - 20 π )