K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

LB
24 tháng 11 2017
\(f=\dfrac{n.p}{60}=\dfrac{3.1200}{60}=60\left(Hz\right)\)
=> C

VT
13 tháng 9 2018
chọn đáp án D
Theo đề ra, có nf - (n-1)f =56 => tần số cơ bản f=56 Hz
=> Tần số họa âm thứ ba f3 = 3f = 3.56 = 168 Hz

HD
Hà Đức Thọ
Admin
3 tháng 6 2016
Câu hỏi của Nguyễn thị phương thảo - Vật lý lớp 12 | Học trực tuyến

SS
2 tháng 6 2016
Ta có: \(\omega=2\pi f=100\pi\left(rad/s\right)\)
Nhiệt lượng
\(Q=I^2Rt=\frac{E^2_0t}{2R}=\frac{\left(\omega NBS\right)^2t}{2R}=\frac{\left(200.100\pi.0,002\right)^2.60}{2.1000}\)\(=474J\)
Nhiệt lượng
\(Q=I^2Rt=\frac{E^2_0t}{2R}=\frac{\left(\omega NBS\right)^2t}{2R}=\frac{\left(200.100\pi.0,002\right)^2.60}{2.1000}\)\(=474J\)
Đáp án B

26 tháng 10 2015
Ban đầu (t=0) dòng điện có giá trị cực đại. Để dòng điện giảm về 0 thì mất thời gian T/4
Suy ra T/4 = 0,004
⇒ T = 0,016s
Tần số f = 1/T = 62,5Hz
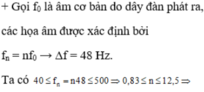

Đáp án C
Hai họa âm liên tiếp nhau là k f 0 , ( k + 1 ) f 0 → ( k + 1 ) f 0 - k f 0 = 56 → f 0 = 56 H z
Họa âm thứ 3 có tần số f 3 = 3 f 0 = 3 . 56 = 168 H z