
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


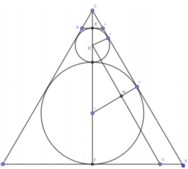
Gọi tâm của hai đường tròn trong (N) là C và D. Ta có GS là tiếp tuyến chung của hai đường tròn tại K và J. Khi đó: D J ⊥ G S C K ⊥ G S
Kẻ D N / / G S ( N ∈ I S ) , khi đó DHKJ là hình chữ nhật nên HK=DJ=1 cm, do đó ta có CH=2 cm.
Ta có ∆ D H C đồng dạng ∆ G J D nên D J C H = G D C D
⇒ D G = D J . C D C H = 1 . 4 2 = 2 cm từ đó suy ra GF = 9 cm.
Ta có ∆ D H C đồng dạng ∆ G F S ⇒ G S D C = G F D H
⇒ G S = D C . G F D H = D C . G F D C 2 - C H 2 = 6 3 cm
⇒ F S = G S 2 - G F 2 = 3 3 cm.
Vì ∆ G E L đồng dạng ∆ G F S nên E L F S = G E G F
⇒ E L = G E . F S G F = 1 . 3 3 9 = 3 3
Vì (N) là khói nón cụt nên:
V N = 1 3 E L 2 + F S 2 + E L . F S E F = 728 π 9
Chọn đáp án D.

Đáp án C
Thể tích của một chòm cầu là V 0 = π h 2 R − h 3 = π .20 2 . 50 − 20 3 = 52000 π 3
Thể tích khối cầu bán kính R = 50 là V = 4 3 π R 3 = 4 3 π .50 3 = 500000 π 3
Suy ra thể tích chum nước là V − 2 × V 0 10 3 = 500000 3 − 2 52000 3 . π 10 3 ≈ 415 lít

Đáp án D.
Khối nón cụt có thể tích là V = πh 3 R 2 + R . r + r 2 mà h = 3 V = π ⇒ R 2 + R . r + r 2 = 1 (*).
Ta có P = R + 2 r ⇔ R = P - 2 r thay vào (*), ta được P - 2 r 2 + P - 2 r r + r 2 = 1
⇔ P 2 - 4 P r + 4 r 2 + P r - 2 r 2 + r 2 - 1 = 0 ⇔ 3 r 2 - 3 P r + P 2 - 1 = 0 (I).
Vậy phương trình (I) có nghiệm khi và chỉ khi ∆ I = - 3 P 2 - 4 . 3 . P 2 - 1 ≥ 0 ⇔ P ≤ 2 .
Vậy giá trị lớn nhất của P là 2.

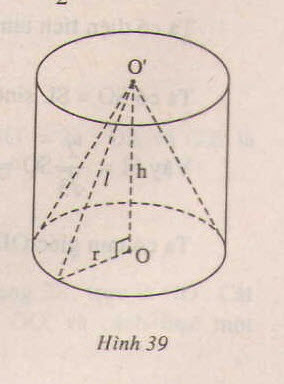
a) Theo đầu bài, hình trụ có chiều cao h = 7 cm và bán kính đáy r = 5 cm.
Vậy diện tích xung quanh bằng: Sxq= πrh = 35π (cm2)
Thể tích của khối trụ là:
V = πr2h = 175π (cm3)
b) Thiết diện là hình chữ nhật có một cạnh bằng chiều cao của hình trụ bằng 7 cm. Giả sử thiết diện là ABCD.
Ta có AD = 7 cm, OI = 3 cm.
Do tam giác OAI vuông tại A nên
AI2 = OA2 – OI2 = 25 – 9 = 16.
Vậy AI = 4 cm, AB = 8 cm.

Đáp án A.
Gọi I là tâm của đường tròn dáy của chỏm cầu. M là 1 đỉnh của hình hộp thuộc đường tròn I ; R 2 .
Ta có:
I M = R 2 ; O M = R ⇒ O I = R 2 − R 2 4 = 3 R 2 .
Do đó khối hộp có chiều cao là
h = 3 R = 10 3 .
Thể tích của chỏm cầu bị cắt:
V = ∫ h 2 R π R 2 − x 2 d x = ∫ 5 3 10 π 100 − x 2 d x ≃ 53 , 87.
Thể tích của khối hộp chữ nhật:
V = S d . h = R 2 2 . 3 . R = 3 2 R 3 ≃ 866 , 025.
Thể tích khối cầu ban đầu:
V = 4 3 π R 3 ≃ 4188 , 79.
Do đó thể tích cần tính:
V ≃ 4188 , 79 − 866 , 025 − 2.53 , 87 ≃ 3215 , 023.