Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

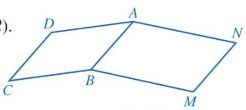
Hai cạnh AB và CD của tứ giác ABCD có song song với nhau.

a, Do ABCD là hình bình hành: AB = CD.
Do ABMN là hình bình hành: AB = MN
Suy ra: CD = MN = AB
b, Do ABCD là hình bình hành \( \Rightarrow \widehat {BCD} = \widehat {DAB}\)
Do ABMN là hình bình hành \( \Rightarrow \widehat {BMN} = \widehat {NAB}\)
\(\widehat {BCD} + \widehat {BMN} = \widehat {DAB} + \widehat {NAB} = \widehat {DAN}\)

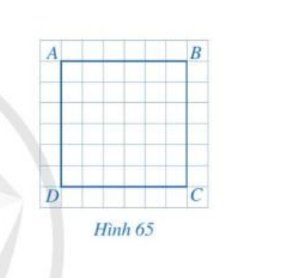
Tứ giác ABCD có: \(\widehat A = \widehat B = \widehat C = \widehat D = {90^o}\)

Do tứ giác ABCD là hình vuông \(\Rightarrow\widehat{CAB}=\widehat{DAC}=\dfrac{\widehat{BAD}}{2}=\dfrac{90^o}{2}=45^o\)

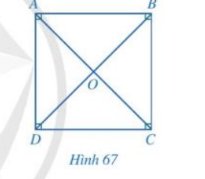
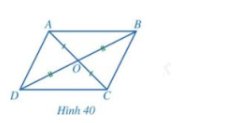
a) Xét hai tam giác ABC và CDA có:AB = CD; AD = BC; AC chung nên \(\Delta ABC = \Delta C{\rm{D}}A(c - c - c)\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CAD}\).
Nên ABCD hình bình hành.
b) Xét hai tam giác ABO và tam giác CDO có: \(OA = OB;\widehat {AOB} = \widehat {CO{\rm{D}}};OC = O{\rm{D}}\)
Suy ra: \(\Delta ABO = \Delta C{\rm{D}}O\)
Suy ra: \(\widehat {BAC}\) = \(\widehat {DCA};\widehat {ACB}\) = \(\widehat {CA{\rm{D}}}\).
Nên ABCD là hình bình hành.

Do tứ giác ABCD là hình vuông nên các cạnh AB, BC, CD, DA bằng nhau và các góc \(\widehat{ABC},\widehat{BCD},\widehat{CDA},\widehat{DAB}\) bằng nhau và bằng 90o.

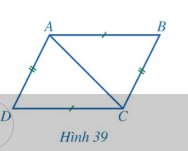
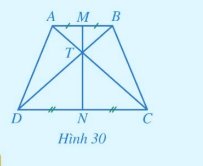
a, Xét \(\Delta ADC\)và \(\Delta BDC\)có:
DC là cạnh chung.
\(\widehat {ADC} = \widehat {BCD}\)(do ABCD là hình thang cân)
AD = BC
\( \Rightarrow \Delta ADC = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {CAD} = \widehat {DBC}\)(2 góc tương ứng) hay
Do: \(\Delta ADC = \Delta BDC\)
Xét \(\Delta BAD\)và \(\Delta ACB\)có:
AB chung
AD = BC
AC = BD
\( \Rightarrow \Delta BDA = \Delta ACB\) (c.c.c)
\( \Rightarrow \widehat {BDA} = \widehat {ACB}\)(2 góc tương ứng) hay \(\widehat {TDA} = \widehat {TCB}\)
b, Xét \(\Delta TAD\)và \(\Delta TBC\)có:
\(\widehat {TAD} = \widehat {TBC}\)(theo câu a)
AD = BC (ABCD là hình thang cân)
\(\widehat {TDA} = \widehat {TCB}\)(theo câu a)
\( \Rightarrow \Delta TAD = \Delta TBC \Rightarrow TA = TB,TC = TD\)
c, Vì: TA = TB \( \Rightarrow \Delta ATB\)cân tại T suy ra TM là trung trực của AB
TC = TD \( \Rightarrow \Delta DTC\)cân tại T suy ra TN là trung trực của CD
Mà: M, T, N thẳng hàng. Nên MN là đường trung trực của cả 2 đường thẳng AB và CD
Vì tứ giác ABCD là hình thang cân nên \(\widehat{ADC}=\widehat{BCD}\).